Contoh Soal Fungsi Komposisi dan Fungsi Invers Lengkap – Bagaimana bentuk contoh soal komposisi itu? Bagaimana bentuk contoh soal fungsi invers itu? Materi fungsi komposisi dan fungsi invers tentunya telah kita pelajari dalam ilmu Matematika. Materi tersebut berisi beberapa pembahasan seperti invers (kebalikan), komposisi (gabungan) dan fungsi (hubungan). Pembahasan ini sangat penting untuk dipelajari karena sering dimasukkan dalam kisi kisi ujian Matematika, baik ujian sekolah maupun ujian Nasional.
Secara umum fungsi dalam Matematika dapat dibagi menjadi dua jenis yaitu fungsi komposisi dan fungsi invers. Kedua jenis fungsi tersebut memiliki definisi dan rumusnya sendiri. Pengertian fungsi komposisi adalah gabungan dari dua fungsi yang memiliki simbol “o”. Dua fungsi yang dimaksud adalah fungsi g(x) dan f(x). Sedangkan pengertian fungsi invers adalah fungsi kebalikan.
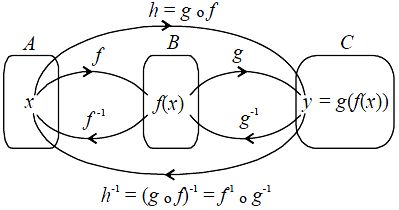
Seperti yang telah kita ketahui bahwa pembelajaran materi fungsi komposisi dan fungsi invers dapat dilakukan dengan mudah. Dalam materi tersebut terdapat penjelasan mengenai contoh soal fungsi komposisi dan fungsi invers. Bagaimana cara menyelesaikan contoh soal fungsi invers itu? Soal soal terkait materi fungsi ini tidak akan lepas dari adanya rumus fungsi yang tersedia. Rumus rumus tersebut digunakan untuk menyelesaikan soal soal fungsi komposisi maupun fungsi invers.
Contoh Soal Fungsi Komposisi dan Fungsi Invers Lengkap
Dalam fungsi invers kita dapat menuliskan fungsi f(x) dan g(x) secara umum dalam bentuk f‾¹(x) maupun g‾¹(x). Selain itu kita juga dapat menyatakan bentuk fungsi identitas denngan lambang I(x) = x. Seperti yang telah kita ketahui sebelumnya bahwa fungsi komposisi dan invers memiliki rumusnya masing masing. Rumus rumus ini sangat penting untuk kita ketahui dan pahami. Pada kesempatan kali ini saya akan membagikan contoh soal fungsi komposisi dan fungsi invers lengkap.
Sifat sifat atau rumus dalam materi fungsi komposisi dan fungsi invers memang dapat dibagi menjadi beberapa macam. Di bawah ini terdapat sifat sifat fungsi komposisi dan fungsi invers yaitu diantaranya:
- Apabila f(x) = ax + b, maka persamaannya menjadi f(g(x)) = a . g(x) + b ataupun f(z) = a . z + b.
- Apabila f(x) = (ax + b) / (cx + d), maka persamaannya menjadi f‾¹(x) = (-dx + b) / (cx – a).
- Apabila f(a) = b, maka persamaannya menjadi f‾¹(b) = a.
- (f ο g)(x) = f(g(x))
- (f ο g)‾¹(x) = (g‾¹ ο f‾¹)(x)
- (f‾¹ ο f)(x) = I(x)
- (f‾¹)‾¹ (x) = f(x)
Sifat sifat yang tertera di atas berguna dalam penyelesaian contoh soal fungsi komposisi dan fungsi invers. Berikut beberapa contoh soal fungsi invers dan contoh soal komposisi yaitu diantaranya:
Baca juga : Materi Kelipatan dan Faktor Bilangan Beserta Contohnya Lengkap
1. Hitunglah fungsi invers f atau f‾¹) dari f(x) = -(4 – 5x) / 4?
Pembahasan.
f(x) = (ax + b) / (cx + d), maka f‾¹(x) = (-dx + b) / (cx – a)
f(x) = -(4 – 5x) / 4 atau f(x) = 5x – 4 / 4
f‾¹(x) = (-4x – 4) / 5
= -4/5 (x + 1)
2. Hitunglah fungsi komposisi (g ο f)(x) apabila diketahui f(x) = 5x + 6 dan g(x) = x² – 5x + 6?
Pembahasan.
Contoh soal fungsi komposisi dan fungsi invers ini dapat diselesaikan dengan langkah seperti di bawah:
(g ο f)(x) = g(f(x))
= g(5x + 6)
= (5x + 6)² – 5(5x + 6) + 6
= 25x² + 60x + 36 – 25x + 30 + 6
= 25x² + 35x + 42
3. Hitunglah fungsi (f ο g)‾¹(x) apabila f(x) = x + 8 dan g(x) = 4x telah diketahui?
Pembahasan.
(f ο g)(x) = f(g(x))
= f(4x)
= 4x + 8
Maka,
(f ο g)(x) = 4x + 8
y = 4x + 8
4x = y – 8
x = (y – 8) / 4
x = ¼y – 2
Jadi (f ο g)‾¹(x) = ¼y – 2.
Baca juga : Cara Mengubah Satuan Kecepatan dan Contoh Soalnya
4. Hitunglah f‾¹(x) apabila f(x) = (7x + 6) / (x + 5) telah diketahui?
Pembahasan .
Contoh soal fungsi komposisi dan fungsi invers ini dapat diselesaikan dengan langkah seperti di bawah:
f(x) = (ax + b) / (cx + d), maka f‾¹(x) = (-dx + b) / (cx – a)
f(x) = (7x + 6) / (x + 5)
f‾¹(x) = (-5x + 6) / (x – 7)
5. Diketahui f(x) = 5x – 1 dan g(x) = 4x² + 5, maka hitunglah nilai komposisi fungsi (g ο f)(1)?
Pembahasan.
(g o f)(x) = g(f(x))
= g(5x – 1)
= 4(5x – 1)² + 5
= 4(25x² – 10x +1) + 5
= 100x² – 40x + 4 + 4
= 100x² – 40x + 8
Maka,
(g ο f)(1) = 100(1)² – 40(1) + 8
= 100 – 40 + 8
= 68
Demikianlah contoh soal fungsi komposisi dan fungsi invers lengkap yang dapat saya bagikan. Materi fungsi komposisi dan fungsi invers mempunyai sifat sifat atau rumus yang harus dipelajari dan dipahami. Semoga artikel ini dapat bermanfaat dan terima kasih telah berkunjung di blog ini.


