Rumus Luas Juring Lingkaran, Contoh Soal, Dan Pembahasannya – Istilah mengenai juring lingkaran tentunya sudah tidak asing lagi untuk kita. Banyak siswa bertanya-tanya bagaimana cara menghitung luas juring lingkaran dengan cepat. Penyebabnya tak lain karena rumus hitung yang cukup kompleks. Beberapa pun sering salah mengartikan dan membedakan antara juring dan tembereng mengingat keduanya berada dalam satu rumpun yang sama.
Cara menyelesaikan contoh soal luas juring lingkaran tidak terlalu sulit asalkan kita tau konsepnya. Bagaimana rumus luas juring lingkaran? Lalu apa yang dimaksud juring lingkaran tersebut? Pengertian juring lingkaran adalah sebuah bidang yang memiliki dua jaring jaring dan dibatasi dengan adanya busur lingkaran. Juring lingkaran tersebut secara umum memang berasal dari fraksi atau pecahan yang terdapat di dalam lingkaran. Bentuk yang dimiliki juring lingkaran ini dapat dimisalkan sebagai bentuk atau potongan kue pie ataupun pizza.
Rumus juring lingkaran sebenarnya sudah mulai disampaikan bahkan semenjak siswa masih berada di bangku SMP. Berbagai model soal dan pembahasannya pun dapat kita temukan pada buku pembelajaran matematika. Semakin berkembangnya teknologi juga membuka jalan untuk mencari rumus cepat serta variasi soal berbeda lewat internet. Oleh karenanya, dalam artikel kali ini marilah kita berfokus pada salah satu pembahasan materi lingkaran yakni luas juring.
Contents
Rumus Luas Juring Lingkaran, Contoh Soal, Dan Pembahasannya
Secara garis besar kita akan menjumpai berbagai pembahasan ketika masuk ke dalam materi juring lingkaran. Oleh karenanya kalian harus benar-benar memperhatikan penjelasan yang disampaikan guru kelas. Di lain sisi, siswa cenderung mengabaikan bahkan menganggap remeh materi satu ini. Padahal mengerjakan soal juring lingkaran dan pembahasannya bukanlah perkara mudah. Alasannya tidak lain karena rumus juring lingkaran begitu sulit untuk dihafalkan mengingat tingkat kompelksitasnya yang tinggi.
Bagaimana rumus luas juring lingkaran itu? Dalam rumus juring lingkaran biasanya memuat busur di dalamnya. Pengertian busur lingkaran tersebut ialah garis lengkung yang terdapat dalam persamaan lingkaran itu sendiri. Biasanya busur yang termuat dalam juring lingkaran dapat berbentuk garis lengkung, baik bentuknya terbuka maupun tertutup. Panjang busur yang dimiliki akan sama dengan keliling lingkarannya apabila garis lengkungnya membentuk lingkaran penuh.
Akan tetapi biasanya sudut yang terbentuk dalam juring lingkaran tersebut dijadikan sebagai fraksi sudut 360°. Lalu bagaimana cara menghitung luas juring lingkaran itu? Bagaimana rumus juring lingkaran itu? Pada kesempatan kali ini saya akan menjelaskan tentang rumus luas juring lingkaran beserta contoh soal luas juring lingkaran. Untuk lebih jelasnya dapat anda simak di bawah ini.
Rumus Juring Lingkaran
Materi satu ini menuntut kita harus hafal rumus luas juring lingkaran dan pembahasannya. Materi ini sering disandingkan dengan materi luas tembereng lingkaran. Untuk itu penting sekali memahami tentang tembereng lingkaran terlebih dahulu. Namun anda juga harus mengetahui apa saja unsur-unsur di dalam lingkaran tersebut. Untuk memahami materi juring lingkaran tersebut, anda dapat memperhatikan gambar di bawah.
Baca juga : Pengertian Bilangan Asli dan Contohnya Terlengkap
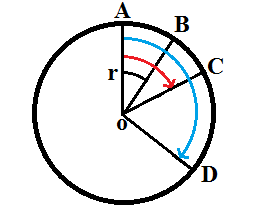
Pada gambar tersebut dapat kita lihat bahwa lingkaran itu memiliki pusat di O dengan jari jari di dalamnya. Gambar ini akan memudahkan anda memahami rumus luas juring lingkaran dan contoh soal luas juring lingkaran nantinya. Kemudian kita juga tahu bahwa lingkaran di atas memiliki sudut AOB (∠AOB) yang terbentuk dari penarikan garis OB sehingga di dalamnya memuat luas juring AOB.
Sudut ini dapat menjadi sudut AOC dan luas juring AOC apabila sudut AOB tadi diperbesar. Kita dapat mencari sudut pusat yang berhubungan dengan juring tersebut menggunakan konsep perbandingan senilai. Untuk itu persamaannya akan seperti berikut:
∠AOB /∠AOC = Luas AOB / Luas AOC
Kita juga dapat menggunakan sudut pusat AOB yang diperbesar dengan luas juring AOB di dalamnya menjadi sudut pusat AOD dengan luas juring AOD tersebut. Jika dijadikan dalam bentuk persamaan, maka akan berbentuk seperti di bawah ini:
∠AOB /∠AOD = Luas AOB / Luas AOD
Bagaimana jika perbesaran sudut pusat AOB dan luas juring AOB dijadikan satu lingkaran penuh? Besar sudut yang termuat dalam lingkaran penuh ini dapat berjumlah 360°. Untuk itu besar luas juringnya disamakan dengan besar luas juring lingkaran penuh tersebut. Pernyataan tersebut dapat dinyatakan dalam bentuk persamaan seperti di bawah ini:
∠AOB / Sudut lingkaran = Luas Juring AOB / Luas lingkaran
∠AOB / 360° = Luas Juring AOB / πr²
∠AOB = (Luas Juring AOB / πr²)360°
atau
Luas Juring AOB = (∠AOB / 360°)πr²
Berdasarkan persamaan tersebut, kita dapat memperoleh kesimpulan bahwa rumus luas juring lingkaran dapat berbentuk seperti di atas. Untuk itu cara menghitung luas juring lingkaran ini dapat dilakukan dengan rumus seperti berikut:
Luas Juring = (α/360°) x πr²
Keterangan:
α = Sudut pusat
π = Phi (22/7 atau 3,14)
r = Jari jari lingkaran
Baca juga : Contoh Soal Sudut Pusat Lingkaran dan Sudut Keliling Lengkap
Contoh Soal Luas Juring Lingkaran
Setelah menjelaskan tentang rumus juring lingkaran di atas. Selanjutnya saya akan membagikan contoh soal juring lingkaran terkait rumus tersebut. Berikut contoh soal dan jawabannya yaitu meliputi:
1. Diketahui sudut pusat lingkaran besarnya 120°. Hitunglah luas juring lingkaran apabila jari jarinya 10 cm?
Jawaban.
Contoh soal luas juring lingkaran ini dapat diselesaikan dengan rumus tertentu. Rumus luas juring lingkaran yang digunakan yaitu:
Luas Juring = (α/360°) x πr²
= (120°/360°) x 3,14 x 10²
= 104,67 cm²
Jadi luas juring lingkaran tersebut ialah 104,67 cm².
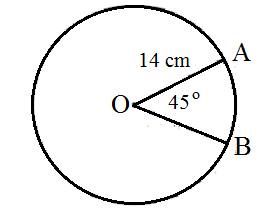
2. Perhatikan gambar berikut!
Hitunglah luas juring lingkaran di atas?
Jawaban.
α = 45°
OB = r = 14 cm
π = 22/7
Luas juring AB = (α/360°) x πr²
= (45°/360°) x 22/7 x 14²
= 77 cm²
Jadi luas juring lingkaran tersebut ialah 77 cm².
Demikianlah penjelasan mengenai rumus luas juring lingkaran beserta contoh soal luas juring lingkaran. Juring lingkaran merupakan sebuah bidang yang memiliki dua jaring jaring dan dibatasi dengan adanya busur lingkaran. Semoga artikel ini dapat bermanfaat dan terima kasih telah membaca materi juring lingkaran di atas.


