Tabel Kebenaran Konjungsi, Disjungsi, Implikasi dan Biimplikasi Lengkap – Bagaimana tabel kebenaran pada konjungsi itu? Bagaimana tabel kebenaran disjungsi? Bagaimana tabel kebenaran implikasi itu? Bagaimana tabel kebenaran biimplikasi itu? Secara umum cakupan yang dimiliki oleh Matematika memang cukup luas. Hal ini dikarenakan dalam ilmu Matematika terdapat cara menghitung ataupun hal hal yang bernuansa angka. Disisi lain Matematika juga membahas tentang ilmu Logika. Dalam materi Logika Matematika tersebut terdapat pembahasan mengenai konjungsi, implikasi, biimplikasi dan disjungsi. Masing masing materi tersebut memiliki tabel kebenarannya sendiri sehingga setiap jenis logika Matematika ini berbeda satu sama lain.
Logika Matematika secara umum merupakan sesuatu hal yang berkaitan dengan pengambilan keputusan. Dalam materi inipun sebenarnya terdapat berbagai hal yang dibahas seperti cara menarik kesimpulan, hubungan dua kalimat atau lebih, ingkaran, pernyataan dan masih banyak lagi. Namun materi yang sering dibahas dalam logika tersebut dapat berupa materi tabel kebenaran konjungsi, tabel kebenaran disjungsi, tabel kebenaran implikasi dan tabel kebenaran biimplikasi. Apa yang dimaksud logika itu? Logika dapat diartikan sebagai cabang ilmu Matematika yang memuat kajian logika dan aplikasi kajian terkait bidang bidang lain diluar Matematika.
Biasanya materi logika Matematika berhubungan dengan ilmu komputer bernuansa kekuatan deduktif dan ilmu logika filosofis sehingga di dalamnya terdapat kekuatan dan pembuktian ekspresif terkait sistem serta logika formalnya. Selain itu dalam materi ini juga terdapat teori pembuktian, teori Matematika konstruktif, teori model, teori rekursi dan teori himpunan di dalamnya. Kemudian dilanjutkan dengan pembahasan materi konjungsi, disjungsi, implikasi dan biimplikasi. Nah pada kesempatan kali ini saya akan menjelaskan tentang tabel kebenaran konjungsi, tabel kebenaran disjungsi, tabel kebenaran implikasi dan tabel kebenaran biimplikasi lengkap. Untuk lebih jelasnya dapat anda simak di bawah ini.
Contents
Tabel Kebenaran Konjungsi, Disjungsi, Implikasi dan Biimplikasi Lengkap
Kegunaan ilmu Logika Matematika ialah untuk menarik kesimpulan berdasarkan premis premis yang dimiliki. Apa yang dimaksud premis itu? Premis ialah pernyaraan dasar yang dianggap benar dalam penarikan kesimpulan. Premis ini biasanya terdapat dalam materi disjungsi, materi biimplikasi, materi konjungsi dan materi implikasi. Masing masing materi ini memiliki pengertian dan tabel kebenarannya sendiri.
Dalam logika Matematika biasanya kita juga menemukan istilah tentang ingkaran atau negasi. Ingkaran atau negasi tersebut merupakan hal pertama yang perlu anda pelajari sebelum memahami tentang konjungsi, disjungsi, implikasi dan biimplikasi. Lantas apa yag dimaksud ingkaran itu? Agar anda lebih paham mengenai materi ini, maka saya akan menyertakan penjelasan mengenai ingkaran atau negasi tersebut dalam artikel ini.
Seperti yang telah kita ketahui bahwa dalam logika Matematika memang terdapat istilah mengenai tabel kebenaran. Tabel kebenaran disini ialah tabel Matematika yang digunakan untuk menjelaskan premis atau pernyataan sesuai dengan nilai kebenarannya. Jika semua hasilnya benar, maka dapat disimbolkan dengan huruf B, T atau 1. Dalam hal ini nilai kebenarannya sering disebut dengan Tautologi. Sedangkan apabila semua hasil akhirnya salah maka dapat disimbolkan dengan huruf S, F atau 0. Dalam hal ini nilai kebenarannya disebut dengan Kontradiksi. Di bawah ini terdapat pembahasan mengenai tabel kebenaran konjungsi, tabel kebenaran disjungsi, tabel kebenaran implikasi dan tabel kebenaran biimplikasi yaitu sebagai berikut:
Ingkaran (Negasi)
Apa yang dimaksud negasi? Negasi ialah kebalikan atau lawan dari sebuah pernyataan. Misalnya pernyataan p bernilai benar, maka negasi pernyataan p ini bernilai salah. Pernyataan negasi itu dapat disimbolkan dengan lambang “~”. Di bawah ini terdapat tabel kebenaran negasi atau ingkaran yaitu:

Dalam tabel kebenaran ingkaran di atas kita dapat melihat nilai benar yang dilambangkan dengan huruf B dan nilai salah dilambangkan dengan hurus S.
Konjungsi
Selanjutnya saya akan membagikan materi logika Matematika yang berupa materi konjungsi. Apa yang dimaksud konjungsi? Konjungsi ialah penggabungan dua pernyataan tunggal dengan kata hubung yang berupa “dan”. Lambang konjungsi ini dapat berupa “^”. Adapun tabel kebenaran konjungsi yaitu sebagai berikut:

Dalam tabel kebenaran tersebut pada dasarnya mengandung hukum yang berbeda. Tabel konjungsi ini memiliki hukum berupa nilai kebenaran konjungsi akan benar apabila kedua pernyataan yang dimiliki bernilai benar. Sedangkan nilai kebenaran konjungsi akan salah apabila terdapat nilai salah satu pernyataan yang salah.
Disjungsi
Selain tabel kebenaran negasi dan tabel kebenaran konjungsi di atas, adapula tabel kebenaran pada materi disjungsi. Apa yang dimaksud disjungsi? Pengertian disjungsi adalah penggabungan dua pernyataan tunggal yang menggunakan kata hubung “atau”. Lambang disjungsi ini dapat berbentuk simbol “v”. Adapun tabel kebenaran disjungsi yaitu sebagai berikut:

Tabel kebenaran di atas memiliki aturannya sendiri yaitu apabila nilai pada kedua pernyataan benar ataupun salah satunya bernilai salah, maka nilai pernyataan disjungsi akan benar. Namun apabila nilai pada kedua pernyataan salah, maka nilai kebenaran disjungsinya akan salah.
Implikasi
Selain tabel kebenaran negasi, tabel kebenaran konjungsi dan tabel kebenaran disjungsi di atas, adapula tabel kebenaran pada materi implikasi. Apa yang dimaksud implikasi? Implikasi adalah penggabungan dua pernyataan yang dilakukan dengan kata hubung “jika” dan “maka”. Simbol implikasi ini dapat dilambangkan dengan tanda “→”. Adapun tabel kebenaran implikasi yaitu:

Tabel kebenaran di atas memuat aturan yang berupa apabila kedua pernyataannya bernilai sama (benar atau salah), maka nilai kebenaran implikasinya benar. Namun apabila kedua pernyataannya memiliki nilai yang berbeda, maka nilai kebenaran implikasinya salah.
Biimplikasi
Selain tabel kebenaran negasi, tabel kebenaran konjungsi, tabel kebenaran disjungsi dan tabel kebenaran implikasi di atas, adapula tabel kebenaran pada materi biimplikasi. Biimplikasi dapat diartikan sebagai penggabungan dua pernyataan tunggal yang menggunakan kata hubung ” jika dan hanya jika, maka”. Lambang biimplikasi ini dapat disimbolkan dengan tanda “↔”. Adapun tabel kebenaran biimplikasi yaitu:

Aturan yang dimiliki tabel kebenaran pada biimplikasi di atas ialah apabila kedua pernyataannya bernilai sama, maka nilai kebenaran biimplikasi benar. Apabila kedua pernyataannya memiliki nilai berbeda, maka nilai kebenaran biimplikasi akan salah.
Negasi Konjungsi
Selain tabel kebenaran negasi, tabel kebenaran konjungsi, tabel kebenaran disjungsi, tabel kebenaran implikasi dan tabel kebenaran biimplikasi di atas, adapula tabel kebenaran pada materi negasi konjungsi. Negasi konjungsi p ∧ q dapat menjadi ~p ∨ ~q. Adapun tabel kebenaran negasi konjungsi yaitu diantaranya:
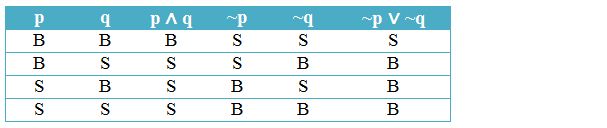
Negasi Disjungsi
Negasi disjungsi p v q dapat berupa ~p ∧ ~q. Nilai equivalen ini dapat dinyatakan dalam bentuk tabel kebenaran negasi disjungsi seperti di bawah ini:
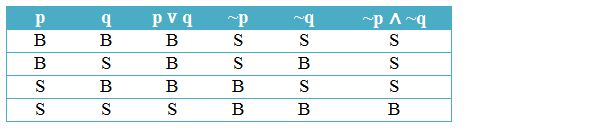
Negasi Implikasi
Selain tabel kebenaran negasi, tabel kebenaran konjungsi, tabel kebenaran disjungsi, tabel kebenaran implikasi, tabel kebenaran biimplikasi, tabel kebenaran negasi konjungsi dan tabel kebenaran negasi disjungsi di atas, adapula tabel kebenaran pada materi negasi implikasi. Implikasi p → q memiliki nilai kebenaran negasi yang berupa p∧~q. Adapun tabel kebenaran negasi implikasi yaitu diantaranya:

Negasi Biimplikasi
Biimplikasi p ↔ q memiliki negasi yang berbentuk (p ∧ ~q) ∨ (q ∧ ~p). Nilai equivalen ini dapat dinyatakan dalam bentuk tabel kebenaran negasi biimplikasi seperti berikut:
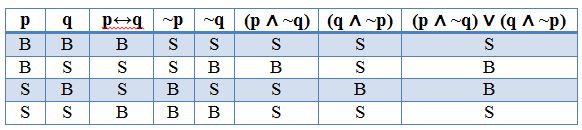
Sekian penjelasan mengenai tabel kebenaran konjungsi, tabel kebenaran disjungsi, tabel kebenaran implikasi dan tabel kebenaran biimplikasi lengkap. Konjungsi, disjungsi, implikasi dan biimplikasi tersebut merupakan salah satu pembahasan mengenai materi logika Matematika. Semoga artikel ini dapat bermanfaat dan terima kasih telah berkunjung di blog ini.


