Rumus Perkalian Matriks, Sifat-Sifat, dan Contoh Soal

Rumus Perkalian Matriks, Sifat-Sifat, dan Contoh Soal – Dalam mata pelajaran Matematika kita sering dibingungkan dengan adanya materi matriks. Secara garis besar, matriks memiliki beberapa operasi hitung berskala cukup luas di dalamnya. Salah satunya ialah operasi hitung perkalian matriks yang notabenya menjadi momok tersendiri untuk sebagian siswa. Banyak siswa gagal mengerjakan soal karena tidak hafal rumus perkalian matriks tersebut.

Taukah kalian apa saja sifat-sifat perkalian matriks matematika? Bagaimana cara menyelesaikan contoh soal perkalian matriks saat ujian? sebenarnya cara menghitung operasi matriks sangatlah mudah. Materi yang termasuk dalam cabang ilmu matematika ini berkaitan dengan kolom dan baris. Maknanya kalian harus menyusun bilangan dalam matriks secara berbaris-baris maupun berkolom-kolom. Metode atau rumus perkalian tersebut juga sering disebut sebagai ordo matriks.

Sebelum mulai menghitung rumus perkalian matriks ada beberapa unsur yang harus kalian pahami terlebih dahulu. Salah satunya adalah sifat matriks itu sendiri yang sedikit banyak akan berpengaruh pada rumus kalian nantinya. Ketika menghadapi contoh soal perkalian matriks pun kalian juga dituntut harus menghafal unsur tersebut. Mengapa demikian? karena susunan bilangan akan disesuaikan dengan sifat-sifat perkalian matriks tersebut.

Rumus Perkalian Matriks, Sifat-Sifat, dan Contoh Soal

Seperti yang kita tahu bahwa dalam ilmu Matematika terdapat materi tentang matriks. Matriks tersebut mengandung beberapa operasi hitung di dalamnya. Salah satunya adalah operasi perkalian matriks yang akan saya bahas ini.

Secara garis besar pengertian matriks memang berupa susunan simbol, karakter atau bilangan menyerupai bangun persegi dalam bentuk baris dan kolom. Kemudian susunan tersebut dibentuk menjadi elemen-elemen untuk selanjutnya dimasukan ke rumus hitung. Sementara itu simbol matriks dalam Matematika dapat dilambangkan dengan huruf kapital, misalnya A, B,C dan sebagainya.

Kemudian untuk tiap elemen matriksnya dapat dilambangkan dengan angka (1, 2, 3, 4 dan sebagainya) maupun dengan huruf kecil (a, b, c, d, dan sebagainya). Seperti yang sudah saya katakan di atas bahwa matriks mengandung ordo di dalamnya. Ordo sendiri dapat diartikan sebagai bilangan yang menunjukkan jumlah baris dan kolom pada matriks.

Contohnya matriks D ordo 4 x 3, maka pada matriks ini terdapat jumlah baris 4 dan jumlah kolom 3. Pada kesempatan kali ini saya akan menjelaskan tentang materi perkalian matriks, rumus perkalian matriks, sifat sifat perkalian matriks dan contoh soal perkalian matriks. Untuk lebih jelasnya dapat anda simak di bawah ini.

Materi Matriks Matematika

Secara umum, matriks memang dapat diartikan sebagai bilangan bilangan yang dikumpulkan untuk disusun berbentuk baris dan kolom serta diapit dengan tanda kurung. Matriks memiliki bilangan yang dapat dikalikan dengan bilangan matriks lainnya. Namun untuk menentukan perkalian matriks ini harus disesuaikan dengan sifat-sifat di dalamnya. Mengingat dimana matriks digunakan untuk menyatakan sebuah pengolahan data secara sederhana untuk berikutnya diselesaikan lagi menggunakan cara yang lebih mudah.

Baca juga : Rumus Barisan dan Deret Geometri Beserta Contoh Soal

Setelah mengetahui pengertian matriks di atas, maka selanjutnya saya akan memberikan pembahasan mengenai rumus perkalian matriks, sifat sifat materi perkalian matriks maupun contoh soal perkalian matriks. Berikut penjelasan selengkapnya:

Sifat Sifat Perkalian Matriks

Ketika membahas perkalian matriks secara tidak langsung kalian sudah terjun pada materi dengan cakupan sangat luas. Karena setipa ordo matriks itu unik dan memiliki rumus hitung yang berbeda satu sama lain. Inilah alasan mengapa banyak siswa mengeluh kesulitan mengerjakan contoh soal perkalian matriks saat ujian.

Rumus tersebut biasanya ditentukan berdasarkan sifat-sifat perkalian matriks itu sendiri. Jadi, kalian tidak bisa seenaknya menghitung bilangan menggunakan satu rumus saja. Seperti yang kita ketahui bahwa perkalian matriks merupakan operasi dua matriks secara biner dalam medan tertentu yang menghasilkan bentuk matriks baru. Adapun sifat-sifat perkalian matriks diantaranya adalah:

1. Bersifat komutatif A + B = B + A (Operasi Penjumlahan).
2. Bersifat asosiatif (A + B) + C = A + (B + C) (Operasi Penjumlahan).
3. Bersifat A + 0 = A (Matriks Nol).
4. Bersifat A + (-A) = 0 (Lawan Matriks).
5. Bersifat asosiatif (AB) C = A (BC) (Operasi Perkalian).
6. Bersifat distributif kiri A(B + C) = AB + AC (Operasi Perkalian).
7. Bersifat k(AB) = (kA)B = A(kB), dimana k = Konstanta Real (Perkalian Matriks dan Konstanta).
8. Bersifat AI = IA = A (Perkalian Matriks Satuan).

Sifat sifat pada perkalian matriks tersebut berguna untuk menyelesaikan berbagai contoh soal perkalian matriks yang ada. Nilai matriks sendiri tidak hanya ditemukan menggunakan sifat saja, namun adapula rumus tertentu yang digunakan. 

Rumus Perkalian Matriks

Operasi hitung matriks dapat dilakukan dengan menggunakan rumus tertentu yang berdasar pada sifat-sifat perkalian matriks pada sesi sebelumnya. Akan tetapi perkalian matriks juga memiliki ketentuan khusus untuk dapat diselesaikan. Membingungkan bukan? matriks memang salah satu materi yang cukup tricky karena memerlukan ketelitian dan hafalan.

Ketentuan perkalian matriks yaitu jumlah kolom pada matriks pertamanya harus sama dengan jumlah baris di matriks kedua. Setelah itu matriks baru dapat dihasilkan dari perkalian tadi, dimana ordonya memiliki jumlah baris yang sama dengan jumlah baris matriks pertama. Untuk lebih jelasnya perhatikan rumus pada perkalian matriks seperti di bawah ini:

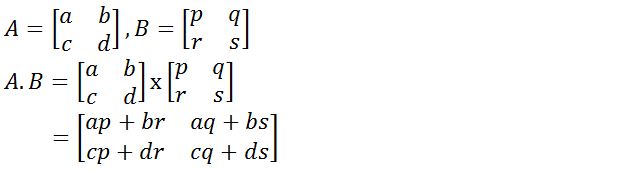
Baca juga : Rumus Skala Beserta Pengertian dan Contoh Soalnya

Simaklah ilustrasi diatas yang menggambarkan rumus perkalian matriks secara gamblang. Ketika mengalami kesulitan menghafalnya lebih baik kalian berlatih mengerjakan soal. Karena dengan berlatih rumus matriks tersebut bisa kalian pahami secara bertahap.

Contoh Soal Perkalian Matriks

Setelah menjelaskan tentang pengertian matriks, sifat sifat matriks dan rumus perkalian matriks di atas. Selanjutnya saya akan membagikan contoh soal terkait materi perkalian matriks tersebut. Berikut contoh soal dan pembahasannya yaitu:

1. Hitunglah perkalian matriks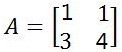dan?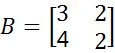

Pembahasan:
Cara menyelesaikan perkalian matriks ini dapat menggunakan rumus matriks seperti di atas. Adapun langkah langkahnya yaitu:

2. Hitunglah perkalian matriks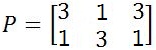dan?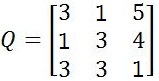

Pembahasan.
Contoh soal perkalian matriks ini dapat diselesaikan dengan cara seperti berikut: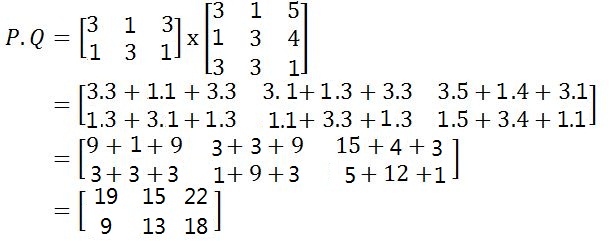

Sekian penjelasan mengenai rumus perkalian matriks, sifat sifat perkalian matriks dan contoh soal perkalian matriks. Perkalian matriks dapat dilakukan apabila jumlah kolom pada matriks pertamanya sama dengan jumlah baris di matriks kedua. Semoga artikel ini dapat bermanfaat dan terima kasih telah membaca materi perkalian matriks di atas.