Sifat Persamaan dan Pertidaksamaan Eksponen dan Penjelasannya – Eksponen menjadi salah satu materi dasar yang diajarkan ketika kita berada di bangku sekolah. Penjelasan mengenai sifat pada persamaan maupun pertidasamaan pun menjadi sangat familiar bagi siswa. Cara menyelesaikan persamaan eksponen dan cara mengerjakan pertidaksamaan eksponen juga turut serta diajarkan oleh guru. Dalam berbagai kesempata kita juga dapat mempelajari beragam variasi contoh soalnya di LKS. Latas, apa yang dimaksud eksponen?
Pengertian eksponen ialah operasi hitung Matematika yang berkaitan erat dengan bilangan pangkat. Cara menghitung bilangan berpangkat ini dapat dilakukan dengan cara mengalikan bilangan sejenis sebanyak jumlah pangkatnya. Misalnya 4² = 4 x 4 = 16. Persamaan dan pertidaksamaan eksponen berkaitan erat dengan penjelasan bentuk operasi hitung perpangkatan. Selain itu adapula penjelasan mengenai sifat sifat persamaan eksponen, sifat sifat pertidaksamaan eksponen, contoh soal persamaan eksponen, contoh soal pertidaksamaan eksponen, cara menyelesaikan persamaan eksponen dan cara menyelesaikan pertidaksamaan eksponen.
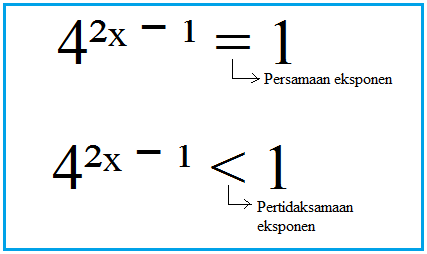
Perbedaan persamaan dan pertidaksamaan eksponen terletak pada tanda hubung di antara ruas-ruasnya. Persamaan eksponen menggunakan tanda hubung berupa sama dengan (=). Sedangkan pertidaksamaan eksponen menggunakan tanda hubung berupa kurang dari (<), lebih dari (>), kurang dari/sama dengan (≤) maupun lebih dari/sama dengan (≥).
Contents
Sifat Persamaan dan Pertidaksamaan Eksponen dan Penjelasannya
Secara umum persamaan dan pertidaksamaan eksponen mengandung bilangan pangkat dan variabel dalam soal soalnya. Nilai variabel ini dapat dihitung dengan cara memenuhi pertidaksamaan maupun persamaan eksponen itu sendiri. Maka dari itulah para siswa harus memahami betul cara menyelesaikan pertidaksamaan eksponen dan cara menyelesaikan persamaan eksponen.
Karena cukup penting akhirnya saya ingin membahas seperti apa sifat persamaan eksponen secara lengkap. Penasaran seperti apa pembahasanya? simaklah artikel di bawah sampai selesai.
Baca juga : Rumus Pertidaksamaan Logaritma Beserta Contoh Soal
Dalam kisi kisi Ujian Nasional dan ujian sekolah Matematika sering kali kita menemukan materi persamaan dan pertidaksamaan eksponen tersebut. Agar anda lebih paham mengenai materi ini, maka saya akan menjelaskan tentang sifat sifat persamaan eksponen, sifat sifat pertidaksamaan eksponen, contoh soal persamaan eksponen dan contoh soal pertidaksamaan eksponen yakni:
Persamaan Eksponen
Persamaan eksponen merupakan dua fungsi yang menggunakan tanda sama dengan pada bilangan berpangkatnya sebagai tanda penghubung diantara keduanya. Misalnya bilangan pangkat pada fungsi linier 6²ˣ ‾ ¹. Persamaan tersebut memiliki nilai x yang memenuhinya yakni x = ½. Dengan begitu persamaan tersebut akan menghasilkan nilai 6⁰ = 1.
Cara menyelesaikan persamaan eksponen pada umumnya dapat dilakukan dengan menggunakan sifat sifat yang tersedia. Sifat sifat persamaan eksponen yang digunakan ini dapat berupa:
- a⁰= 1
- a‾¹ = 1/a
- aᵐ × aⁿ = aᵐ ⁺ ⁿ
- aᵐ : aⁿ = aᵐ ‾ ⁿ
- (aᵐ)ⁿ = aᵐ ˣ ⁿ
- (aᵐ × aⁿ)ᵖ = aᵖᵐ ⁺ᵖⁿ
Selain itu adapula sifat fungsi persamaan eksponen yang digunakan untuk menyelesaikan contoh soal persamaan eksponen. Sifat sifat fungsi tersebut dapat meliputi:
- Apabila aᶠ⁽ˣ⁾ = aᴾ, maka f(x) = P
- Apabila aᶠ⁽ˣ⁾ = aᶢ⁽ˣ⁾, maka f(x) = g(x)
Agar anda lebih paham mengenai persamaan eksponen tersebut. Saya akan menjelaskan tentang penjabaran contoh persamaan eksponen menggunakan sifat sifat persamaan eksponen di atas. Berikut cara menyelesaikan persamaan eksponennya yaitu:
6²ˣ ‾ ¹ = 1
6²ˣ ‾ ¹ = 6⁰
2x – 1 = 0
2x = 1
x = ½
Baca juga : Contoh Soal Bilangan Berpangkat Beserta Jawaban dan Pembahasannya
Pertidaksamaan Eksponen
Pembahasan berikutnya saya akan membahas tentang sifat sifat pertidaksamaan eksponen. Cara menyelesaikan pertidaksamaan eksponen secara umum memang hampir sama dengan cara menyelesaikan persamaan eksponen. Karakteristik yang dimiliki oleh pertidaksamaan eksponen tersebut ialah tanda hubung yang digunakan oleh dua fungsi bilangan pangkat. Tanda pertidaksamaan yang digunakan dapat berupa <, >, ≤ dan ≥.
Sifat sifat yang digunakan dalam pertidaksamaan eksponen dapat berupa::
Untuk a ≥ 1 meliputi:
- aᶠ⁽ˣ⁾ < aᶢ⁽ˣ⁾ → f(x) < g(x)
- aᶠ⁽ˣ⁾ > aᶢ⁽ˣ⁾ → f(x) > g(x)
- aᶠ⁽ˣ⁾ ≤ aᶢ⁽ˣ⁾ → f(x) ≤ g(x)
- aᶠ⁽ˣ⁾ ≥ aᶢ⁽ˣ⁾ → f(x) ≥ g(x)
Untuk a < a < 1 meliputi:
- aᶠ⁽ˣ⁾ < aᶢ⁽ˣ⁾ → f(x) > g(x)
- aᶠ⁽ˣ⁾ > aᶢ⁽ˣ⁾ → f(x) < g(x)
- aᶠ⁽ˣ⁾ ≤ aᶢ⁽ˣ⁾ → f(x) ≥ g(x)
- aᶠ⁽ˣ⁾ ≥ aᶢ⁽ˣ⁾ → f(x) ≤ g(x)
Selain sifat sifat pertidaksamaan eksponen tersebut adapula contoh soal pertidaksamaan eksponen beserta jawabannya. Berikut contoh soalnya yaitu:
Hitunglah nilai x yang memenuhi pertidaksamaan 6²ˣ ‾ ¹ < 1?
Jawaban.
6²ˣ ‾ ¹ < 1
6²ˣ ‾ ¹ < 3⁰
2x – 1 < 0
2x < 1
x < ½
Jadi nilai x yang memenuhi pertidaksamaan 6²ˣ ‾ ¹ < 1 yaitu x < ½.
Seperti yang telah kita ketahui bahwa perbedaan persamaan dan pertidaksamaan eksponen terletak pada penggunaan tanda dan hasil akhir keduanya. Persamaan eksponen memiliki hasil akhir yang berupa suatu bilangan. Sedangkan hasil akhir dalam pertidaksamaan eksponen dapat berupa derah penyelesaian pada pertidaksamaan yang memenuhinya. Demikianlah penjelasan mengenai sifat sifat persamaan eksponen dan sifat sifat pertidaksamaan eksponen lengkap. Semoga artikel ini dapat bermanfaat dan terima kasih telah berkunjung di blog ini.


