Luas Segi n Beraturan dan Keliling Beserta Contoh Soal – Segi n beraturan pada umumnya terbagi menjadi beberapa jenis seperti segitiga, segiempat, segi lima, segi enam, seni tujuh, segi delapan dan sebagainya. Segi n beraturan ini memiliki rumus yang berbeda-beda. Bagaimana rumus segi n beraturan itu? Bangun datar segi n beraturan pada umumnya berasal dari lingkaran yang dibagi menjadi beberapa bagian yang besarnya sama sehingga bentuknya menyerupai segitiga sama kaki.
Bagaimana cara menentukan segi n beraturan dalam matematika? Itulah pertanyaan yang sering diajukan siswa. Ketika membahas pelajaran matematika kita memang akan dihadapkan dengan rumus hitung, latihan soal, dan lain sebagainya. Salah satu pembahasan yang menurut saya penting ialah materi segi n beraturan. Dalam materi ini terdapat beberapa rumus di dalamnya yaitu rumus luas segi n beraturan dan rumus keliling segi n beraturan. Tidak jarang pula kita menemukan contoh soal segi n beraturan dalam ujian seperti UAS maupun UTS.
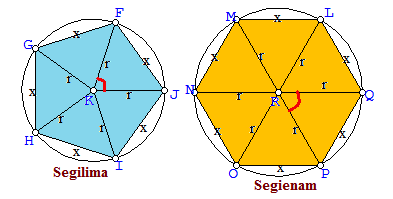
Segi n beraturan memang berasal dari bagian-bagian kecil pada lingkaran. Untuk itu rumus segi n beraturan melibatkan jari jari dan sudut pusat di dalamnya. Sudut pusat ialah sudut segitiga (dinyatakan dalam tanda sudut berwarna merah) yang memiliki besar 360°/n. Selain itu dalam bangun datar segi n beraturan terdapat sisi yang dinyatakan dalam bentuk x. Untuk lebih jelasnya perhatikan gambar di bawah ini.
Bangun datar segi n beraturan dapat dihitung luas dan kelilingnya menggunakan rumus pada luas segitiga dengan sudut di dalamnya. Untuk itu terdapat peran aturan sinus pada perhitungan luasnya dan aturan kosinus pada perhitungan kelilingnya.
Contents
Luas Segi n Beraturan dan Keliling Beserta Contoh Soal
Karena dalam rumus segi n beraturan terdapat peran aturan sinus dan kosinus di dalamnya, maka alangkah lebih baik jika anda memahami tentang nilai perbandingan trigonometri terlebih dahulu yang berkaitan dengan sudut sudut istimewa. Pada kesempatan kali ini saya akan menjelaskan tentang rumus luas segi n beraturan dan rumus keliling segi n beraturan beserta contoh soal.
Secara umum pengertian segi n beraturan ialah segi banyak yang memiliki sisi semuanya dengan panjang sama dan besar semua sudutnya sama. Selain itu adapula yang mengatakan bahwa segi n beraturan ialah bangun datar yang mempunyai jumlah sisi lebih dari empat segi dan mempunyai segi beraturan di dalamnya. Adapun contoh segi n beraturan tersebut yaitu segi sepuluh beraturan, segi enam beraturan, segidelapan beraturan dan lain lain.
Seperti yang telah kita tahu bahwa rumus luas segi n beraturan melibatkan aturan sinus di dalamnya. Sedangkan rumus keliling segi n beraturan melibatkan aturan kosinus di dalamnya. Untuk itulah kedua rumus segi n beraturan tersebut berkaitan dengan luas pada segitiga yang mengandung sudut sudut istimewa di dalamnya. Adapun rumus dan contoh soal seni n beraturan yaitu sebagai berikut:
Luas Bangun Datar Segi n Beraturan
Untuk menghitung luas pada segi n beraturan dapat dilakukan dengan menggunakan rumus luas segitiga dengan aturan sinus di dalamnya. Adapun rumus segitiganya yaitu meliputi:
Luas Segitiga = ½.r.r.sin θ = ½ r² sin 360°/n
Rumus luas segitiga menggunakan aturan sinus di atas dapat digunakan untuk menghitung luas pada segi n beraturan. Adapun rumus luas segi n beraturan yaitu sebagai berikut:
Luas segi n = n × Luas Segitiga
Luas segi n = n/2 r² sin 360°/n
Keliling Bangun Datar Segi n Beraturan
Selain rumus luas bangun datar segi n beraturan di atas, adapula rumus keliling segi n beraturan. Panjang segi n (x) dapat dihitung menggunakan aturan kosinus. Panjang x menurut aturan kosinus dalam segitiga PRQ dapat dihitung dengan persamaan seperti di bawah ini:
Dari persamaan di atas dapat diperoleh rumus keliling segi n beraturan seperti di bawah ini: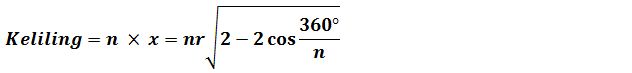
Keterangan:
θ = Sudut pusat yang besarnya 360º/n
Contoh Soal Luas dan Keliling Segi n Beraturan
Setelah menjelaskan tentang rumus luas segi n beraturan dan rumus keliling segi n beraturan di atas. Selanjutnya saya akan membagikan contoh soal segi n beraturan seperti di bawah ini:
1. Tentukan luas dan keliling segi enam beraturan yang jari jarinya memiliki panjang 20 cm?
Pembahasan.
Contoh soal tersebut dapat diselesaikan dengan rumus segi n beraturan seperti di bawah ini:
n = 6 (karena bentuknya segienam)
r = 20 cm
Sehingga,
Luas segienam = n/2 r² sin 360°/n
= 6/2 20² sin 360°/6
= 600 sin 60
= 600 ½√3
= 300√3 cm²
Keliling = nr √(2 – 2 cos 360°/n)
=6.20 √(2 – 2 cos 360°/6)
= 120 √(2 – 2.½)
= 120 √(2 -1)
= 120 √1
= 120 cm
Jadi luas dan keliling segi enam beraturan 300√3 cm² dan 120 cm.
2. Bangun datar segi 12 beraturan memiliki besar luas 48 cm². Maka tentukan:
a. Panjang sisi dan panjang jari jari
b. Keliling segi 12 beraturan
Pembahasan.
a. Contoh soal segi n beraturan tersebut dapat diselesaikan dengan rumus tertentu. Adapun rumus luas segi n beraturan yaitu sebagai berikut:
Luas Segi 12 = n/2 r² sin 360°/n
48 = 12/2 r² sin 360°/12
48 = 6r² sin 30
48 = 6r² ½
48 = 3r²
r² = 16
r = 4 cm
Maka,
Panjang sisi segi 12 = r√(2 – 2 cos 360°/n)
= 4√(2 – 2 cos 360°/12)
= 4√(2 – 2 cos 30°)
= 4√(2 – 2.½√3)
= 4√(2 – √3)
b. Selanjutnya menggunakan rumus keliling segi n beraturan dengan beberapa langkah seperti di bawah ini:
Keliling = n.x
= 12.4√(2 – √3)
= 48√(2 – √3)
Demikianlah penjelasan mengenai rumus luas segi n beraturan dan rumus keliling segi n beraturan beserta contoh soal segi n beraturan. Segi n beraturan merupakan segi banyak yang memiliki sisi semuanya dengan panjang sama dan besar semua sudutnya sama. Semoga artikel ini dapat bermanfaat dan terima kasih telah membaca materi segi n beraturan di atas.


