Rumus Trigonometri Lengkap Dengan Contoh Soal – Dalam pembelajaran Matematika terdapat pembahasan mengenai materi trigonometri. Apa yang dimaksud trigonometri itu? Bagaimana cara menyelesaikan contoh soal trigonometri itu? Trigonometri merupakan cabang ilmu Matematika yang membahas tentang hubungan panjang sisi dengan besar sudut pada segitiga. Misalnya tangen, sinus dan cosinus. Dalam bahasa Yunani secara harfiah, trigonometri berasal dari kata “Trogonom” yang maknanya tiga sudut dan kata “Metron” berarti mengukur. Trigonometri ini memiliki rumusnya sendiri seperti halnya pada materi dalam Matematika lainnya. Rumus inilah yang nantinya dapat digunakan untuk menyelesaikan soal soal trigonometrinya.
Dalam rumus trigonometri terdapat identitas yang menyatakan hubungan atau relasi mengandung fungsi trignometri yang saling berkaitan satu sama lain. Nah, mari kita sepakat untuk menyebutnya sebagai indentitas trigonometri. Umumnya Para ahli Matematika menggunakan trigonometri untuk mengetahui fenomena yang berkaitan dengan panjang serta sudut segitga.
Dalam Trigonometri kalian akan menemukan konsep dasar berupa kesebangunan sisi-sisi bersesuaian dan kesebangunan segitiga siku siku, dimana nilai perbandingannya sama. Dalam dua segitiga sendiri terdapat besar sudut yang sama pada konsep geometri euclid. Untuk itu terdapat konsep kesebangunan pada kedua segitiganya. Bagaimana bentuk contoh soal trigonometri itu?
Rumus Trigonometri Beserta Contoh Soalnya
Materi trigonometri memang erat kaitannya dengan tabel sin cos tan. Ketika dibangku sekolah menengah atas, para siswa memang sudah diajarkan mengenai Trigonometri Matematika yang memuat beberapa rumus di dalamnya. Bahkan materi ini juga sering dijadikan bahan soal soal ujian Matematika, baik ujian Nasional maupun ujian Sekolah.
Konsep trigonometri memang lebih berkaitan dengan konsep segitiga secara penting. Perumusan nilai nilai trigonometri dapat disesuaikan dengan perbandingan panjang sisi yang terdapat pada segitiga siku siku. Nah pada kesempatan kali ini saya akan menjelaskan tentang rumus trigonometri lengkap dengan contoh soal trigonometri.
Seperti yang telah kita ketahui bahwa dalam perbandingan trigonometri terdapat beberapa nilai seperti sin (sinus), cos (cosinus), tan (tangen), sec (secan), cot (cotangen) dan cosec (cosecan). Cara menentukan nilai nilai trigonometri ini dapat dilakukan dengan menggunakan aturan tertentu untuk membandingkan panjang sisi segitiga. Trigonometri memang banyak digunakan dalam bidang geografi, akustik, elektronik, statistika, pencitraan medis, kimia, astronomi, teori musik, topik analisis pasar finansial, teori probabilitas, biologi, farmasi dan sebagainya.
Baca juga : Rumus Frekuensi Harapan, Cara Menghitung dan Contoh Soal
Ketika berurusan dengan studi tentang panjang dan sudut segitiga, kita tidak akan lepas pula dari beberapa unsur didalamnya. Salah satunya adalah identitas trigonometri yang sedikit banyak berfungsi menghitung sin cos tan. Selain mengajarkan rumus hitung, saya juga telah mempersiapkan beberapa contoh soal trigonometri dengan tingkat kesulitan setara UAS, UTS, dan UN. Maka dari itu simaklah artikel kali ini sampai selesai.
Rumus Trigonometri Sin Cos Tan
Sinus, cosinus, dan tangen adalah tiga rumus utama dalam materi trigonometri SMA maupun SMK. Kalau boleh jujur menghitung sin cos tan adalah hal yang saya tidak suka karena tingkat kerumitannya. Maka dari itu, kalian harus memperhatikan baik-baik penjelasan rumus sin cos tan karena materi trigonometri benar-benar membutuhkan ketelitian ekstra.
Dalam konsep trigonometri terdapat sisi sisi segitiga siku siku menurut letaknya terhadap sudut yang dibandingkan seperti sisi samping, sisi miring dan sisi depan. Sisi depan ialah sisi yang letaknya di depan sudut. Sisi samping ialah sisi yang letaknya di samping sudut. Sedangkan sisi miring ialah sisi yang berada di depan sudut 90º.
Dari perbandingan ini akan ditemukan fungsi trigonometri utama yang meliputi fungsi cos, fungsi tan dan fungsi sin. Ketiga fungsi ini disesuaikan dengan sudut dan sisi pada segitiga siku siku. Konsep inilah yang nantinya akan berperan dalam rumus trigonometri dan cara menyelesaikan contoh soal trigonometri. Untuk lebih jelasnya perhatikan gambar di bawah ini:
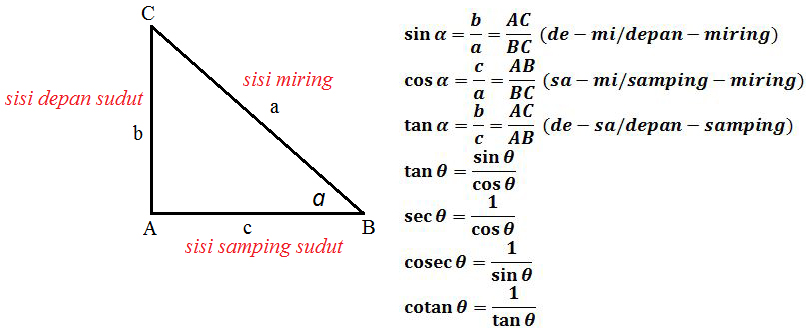
Berdasarkan persamaan di atas, kita dapat menemukan nilai nilai trigonometri pada sudut istimewa seperti di bawah ini:
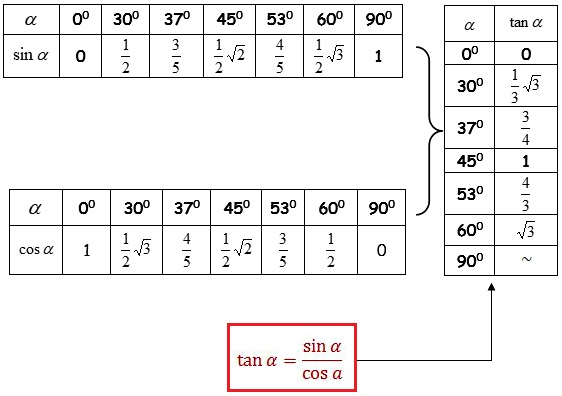
Pemahaman tentang nilai-nilai trigonometri pada sudut istimewa sangat berguna dalam perhitungan trigonometri yang lebih kompleks. Faktanya, kita dapat menggunakan rumus rumus trigonometri sin cos tan untuk menyelesaikan berbagai masalah geometri. Seperti menghitung panjang sisi segitiga, menentukan sudut untuk navigasi, dan lain sebagainya.
Perbandingan Trigonometri Sudut Berelasi
Sebelum membahas tentang rumus trigonometri dan contoh soal trigonometri tersebut, saya akan menjelaskan terlebih dahulu mengenai perbandingan trigonometri pada sudut berelasi. Perbandingan ini ialah perluasan dari penentuan nilai trigonometri dasar yang berasal dari sudut segitiga siku siku.
Dalam konsep ini terdapat kuadran 1 yang memuat sudut segitiga dengan besar siku siku. Konsep kuadrat 1 muncul karena ukurannya ada di 0º – 90º serta tergolong dalam sudut lancip. Sedangkan jika besarnya 0º – 360º maka dapat disebut dengan sudut pusat lingkaran. Di bawah ini terdapat gambar letak masing masing kuadran yaitu:

Berdasarkan gambar di atas, kita dapat menyimpulkan beberapa hal seperti di bawah ini:
- Kuadran 1 memiliki nilai perbandingan trigonometri yang semuanya positif, dimana besar sudutnya diantara 0° – 90°.
- Kuadran 2 memiliki nilai perbandingan trigonometri yang cosecan dan sin positif, dimana besar sudutnya diantara 90° – 180°.
- Kuadran 3 memiliki nilai perbandingan trigonometri yang cotangen dan tangen positif, dimana besar sudutnya diantara 180° – 270°.
- Kuadran 4 memiliki nilai perbandingan trigonometri yang secan dan cosinus positif, dimana besar sudutnya diantara 270° – 360°.
Baca juga : Contoh Soal Perbandingan Senilai Beserta Pembahasan Lengkap
Identitas Trigonometri
Rumus trigonometri selanjutnya berkaitan dengan materi identitas trigonometri. Identitas menggunakan dasar penyusunan dari konsep teorema phytagoras seperti a² + b² = c². Identitas trigonometri adalah hubungan salah satu fungsi trigonometri dengan fungsi lainnya. Jika sinus kuadrat dijumlahkan dengan cosinus kuadrat maka hasilnya sama dengan satu.
Apabila cosinus kuadrat membagi kedua ruasnya, maka akan memperoleh penambahan satu dengan tangen kuadrat sehingga hasilnya sama dengan secan kuadrat. Berbeda lagi jika sinus kuadrat membagi kedua ruas, maka akan memperoleh penambahan cosecan kuadrat atau cotangen kuadrat. Adapun rumus identitas trigonometri yaitu sebagai berikut:

Rumus Trigonometri Lainnya
Dalam trigonometri tersebut tidak hanya rumus identitas yang meliputi sin cos tan saja. Namun adapula beberapa rumus hitung lain yang sering dipakai ketika ujian berlangsung. Secara tidak langsung, siswa pun diwajibkan untuk menghafal rumus trigonometri tersebut agar lancar mengerjakan soal latihan maupun ujian.
Rumus Jumlah dan Selisih Sudut
Simaklah cara mencari jumlah dan selisih sudut trigonometri pada ilustrasi rumus di bawah:
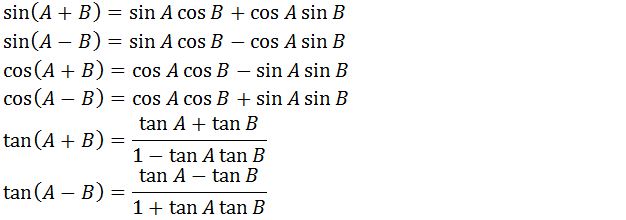
Rumus Perkalian Trigonometri
Simaklah cara menghitung perkalian trigonometri pada ilustrasi rumus di bawah:
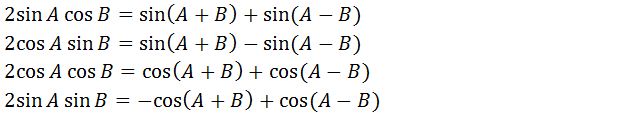
Rumus Jumlah dan Selisih Trigonometri
Simaklah cara menghitung jumlah dan selisih trigonometri pada rumus di berikut:
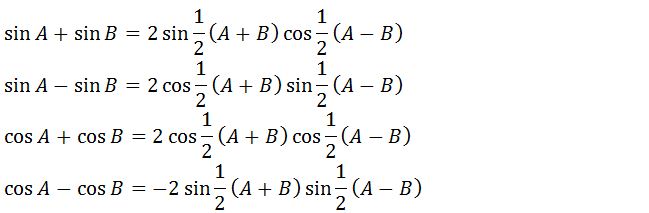
Contoh Soal Trigonometri
Sebenarnya kalian bisa menemukan contoh soal trigonometri SMA dan SMP dengan level berbeda pada buku pembelajaran. Guru pun pasti akan membahas materi trigonometri secara intensif dan berulang mengingat besarnya peran materi satu ini dalam ujian.
Setelah menjelaskan tentang rumus trigonometri di atas. Selanjutnya saya akan membagikan contoh soal terkait rumus tersebut. Berikut contoh soal dan pembahasannya:
Tentukan nilai dari 2cos 45º cos 15º?
Pembahasan.
Contoh soal trigonometri tersebut menggunakan konsep perkalian trigonometri. Untuk itu rumusnya dapat menjadi seperti di bawah ini:
2 cos A cos B = cos (A + B) + cos (A – B)
2cos 45º cos 15º = cos (45 +15)° + cos (45 – 15)°
= cos 60° + cos 30°
= ½√2 + ½√3
Jadi nilai dari 2cos 45º cos 15º ialah ½√2 + ½√3.
Demikianlah penjelasan mengenai rumus trigonometri lengkap dengan contoh soal trigonometri. Trigonometri merupakan salah satu materi Matematika yang berhubungan dengan sudut sudut istimewa dan sisi sisi pada segitiga. Semoga artikel ini dapat bermanfaat dan terima kasih telah berkunjung di blog ini.


