Pengertian Fungsi Komposisi, Rumus, Sifat dan Contoh Soal – Apa yang dimaksud materi fungsi komposisi itu? Bagaimana rumus fungsi komposisi? Bagaimana sifat sifat fungsi komposisi itu? Bagaimana cara menyelesaikan contoh soal fungsi komposisi itu? Fungsi komposisi merupakan salah satu materi Matematika yang diajarkan ketika di bangku sekolah. Materi ini sering dikaitkan dengan fungsi invers Matematika. Maka dari itu anda perlu memahami materi fungsi invers ini sebelum mempelajari materi tentang fungsi komposisi tersebut. Dengan begitu pemahamannya dapat dilakukan dengan mudah.
Seperti yang telah saya katakan di atas bahwa materi fungsi komposisi memuat beberapa hal yang dibahas. Pembahasan ini dapat meliputi pengertian fungsi komposisi, rumus fungsi komposisi, sifat sifat fungsi komposisi dan contoh soal fungsi komposisi. Fungsi komposisi merupakan fungsi baru dari fungsi g(x) dan fungsi f(x) yang digabungkan menjadi satu. Operasi pada fungsi komposisi tersebut dapat dinotasikan dalam bentuk huruf atau simbol “o”. Simbol atau huruf ini dapat dibaca dengan komposisi atau bundaran.
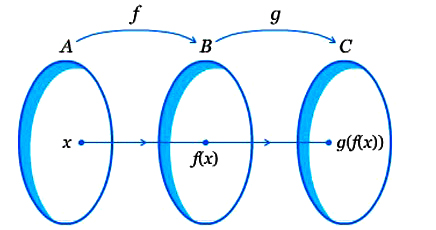
Kita tahu bahwa dua fungsi tertentu dapat digabungkan menjadi satu dalam bentuk sebuah fungsi komposisi. Fungsi yang dimaksud tersebut ialah fungsi g(x) dan fungsi f(x). Untuk melakukan operasi fungsi komposisi tentunya diperlukan cara tertentu. Nah pada kesempatan kali ini saya akan menjelaskan tentang pengertian fungsi komposisi, rumus fungsi komposisi, sifat sifat fungsi komposisi dan contoh soal fungsi komposisi. Untuk lebih jelasnya dapat anda simak di bawah ini.
Contents
Pengertian Fungsi Komposisi, Rumus, Sifat dan Contoh Soal
Ketika dibangku sekolah tentunya kita mengenal tentang istilah fungsi. Salah satu jenis fungsi yang akan saya bahas ini berkaitan dengan fungsi ekonomi. Fungsi adalah relasi yang terjadi pada himpunan A dan himpunan B, dimana masing masing anggota A dipasangkan tepat dengan satu anggota B. Untuk penerapannya terdapat komposisi yang berhubungan dengan lebih dari satu fungsi.
Ketika satu fungsi dilanjutkan ke fungsi lainnya, maka akan menghasilkan sebuah fungsi baru. Fungsi baru tersebut dikenal dengan nama fungsi hasil komposisi dari kedua fungsi yang sebelumnya digunakan. Sebuah pemetaan atau fungsi dapat disajikan dalam bentuk rumus, diagram cartesius, pasangan berurut, ataupun diagram panah.
Agar anda lebih paham mengenai materi fungsi komposisi tersebut, maka saya akan menjelaskan pengertian, rumus, sifat, dan contoh soal di dalamnya. Adapun pengertian fungsi komposisi, rumus fungsi komposisi, sifat sifat fungsi komposisi dan contoh soal fungsi komposisi yaitu sebagai berikut:
Pengertian Fungsi Komposisi
Apa pengertian fungsi komposisi itu? Fungsi komposisi dapat didefinisikan sebagai fungsi baru dari fungsi g(x) yang digabungkan dengan fungsi f(x). Fungsi baru dari g(x) dan f(x) yang terbentuk ini dapat berupa:
- (g o f)(x) = f dimasukkan ke g
- (f o g)(x) = g dimasukkan ke f
Baca juga : Rumus Jarak, Kecepatan, dan Selisih Waktu Beserta Contoh Soal
Dari pengertian fungsi komposisi di atas kita tahu bahwa terdapat fungsi tertentu di dalamnya. Fungsi yang dimaksud ialah fungsi tunggal. Fungsi tunggal merupakan sebuah fungsi dengan simbol berbentuk “f o g”. Simbol ini dapat diartkan sebagai fungsi f bundaran g. Untuk penyelesaian dalam materi fungsi komposisi dengan bentuk tersebut harus mencari terlebih dahulu fungsi g nya, lalu baru menentukan fungsi f nya.
Kemudian adapula bentuk fungsi “g o f” yang dibaca g bundaran f. Untuk itu kita dapat mencari fungsi f dan kemudian dilanjutkan fungsi g nya. Di bawah ini terdapat pembahasan tentang rumus fungsi komposisi, sifat sifat fungsi komposisi dan contoh soal fungsi komposisi yaitu sebagai berikut:
Rumus Fungsi Komposisi
Fungsi komposisi memiliki rumus tertentu yang digunakan untuk menyelesaikan soal soal yang tersedia. Adapun rumus yang digunakan dalam fungsi komposisi tersebut yaitu:
y = f(x) jika f : A → B
y = g(x) jika g : B → A
Kemudian hasil fungsi g dan f tersebut berdasarkan rumus di atas dapat berbentuk seperti di bawah ini:
h(x) = (g o f)(x) = g(f(x))
Fungsi g dan fungsi f yang termuat dalam fungsi komposisi ini dapat diperjelas lagi dalam bentuk seperti berikut:
(g o f)(x) = g(f(x))
(f o g)(x) = f(g(x))
Baca juga : Contoh Soal Fungsi Invers, Jawaban, dan Pembahasannya
Sifat Sifat Fungsi Komposisi
Selain pengertian fungsi komposisi dan rumus fungsi komposisi di atas. Adapula sifat sifat pada materi fungsi komposisi ini. Fungsi komposisi memiliki beberapa sifat jika bentuknya f : A → B , g : B → C , h : C → D yakni:
- Sifat komutatif (f o g)(x) ≠ (g o f)(x) tidak diberlakukan.
- Sifat asosiatif [f o (g o h)(x)] = [(f o g ) o h (x)] tersebut dapat dimiliki.
- Memiliki fungsi identitas I (x) yang bentuknya (f o l)(x) = (l o f)(x) = f(x).
Contoh Soal Fungsi Komposisi
Agar anda lebih paham mengenai pengertian fungsi komposisi, rumus dan sifat sifat fungsi komposisi di atas. Maka saya akan membagikan beberapa contoh soal terkait materi tersebut. Berikut contoh soal dan jawabannya yaitu:
Diketahui fungsi f(x) dan g(x) secara berturut turut dalam bentuk f(x) = 6x + 5 dan g(x) = 5 – x. Hitunglah nilai dari:
1. (f o g)(x)
2. (g o f)(x)
Jawaban.
Contoh soal fungsi komposisi tersebut dapat diselesaikan dengan cara berikut:
f(x) = 6x + 5
g(x) = 5 – x
Maka,
1. (f o g)(x) = f(g(x)) → g(x) masuk ke dalam f(x)
= f (5 – x)
= 6 (5 – x) + 5
= 30 – 6x + 5
= -6x + 35
2. (g o f)(x) = g(f(x)) → f(x) masuk ke dalam g(x)
= g (6x + 5)
= 5 – (6x + 5)
= 5 – 6x + 5
= -6x
Sekian penjelasan mengenai pengertian fungsi komposisi, rumus fungsi komposisi, sifat sifat fungsi komposisi dan contoh soal fungsi komposisi. Materi fungsi komposisi di atas merupakan fungsi baru dari fungsi g(x) yang digabungkan dengan fungsi f(x). Semoga artikel ini dapat bermanfaat dan terima kasih telah berkunjung di blog ini.


