Rumus Kerucut (Luas Permukaan dan Volume) Beserta Contoh Soal – Kerucut merupakan satu dari sekian jenis bangun ruang yang memiliki rumus luas dan rumus volume. Bagaimana rumus luas permukaan kerucut itu? Bagaimana rumus volume kerucut itu? Bagaimana cara menyelesaikan contoh soal kerucut? Apa yang dimaksud kerucut itu? Pengertian kerucut ialah bangun tiga dimensi yang mempunyai dua sisi berupa sisi lengkung dan sisi lingkaran. Dalam kerucut terdapat lingkaran yang secara umum berperan sebagai alas. Sedangkan bidang lengkungnya mengarah pada titik tertentu yang berupa puncak dari kerucut itu sendiri.
Dalam pembelajaran Matematika tersebut terdapat pembahasan mengenai rumus kerucut yang mencakup rumus luas permukaan kerucut, rumus volume kerucut dan cara menyelesaikan contoh soal kerucut. Disisi lain kerucut juga dapat diartikan sebagai jenis limas istimewa. Dalam bahasa Inggris, kerucut tersebut dapat dinamakan dengan cone. Kerucut memang dapat dikategorikan sebagai limas dengan bentuk alas berupa lingkaran. Selain itu adapula limas yang alasnya segi n, dimana bentuk sisi tegaknya berupa segitiga. Namun karena kerucut tersebut memiliki alas berbentuk lingkaran, maka sisi tegak yang dimilikinya berbentuk lengkungan.
Seperti yang telah kita ketahui bahwa dalam materi kerucut tersebut terdapat pembahasan mengenai pengertian kerucut dan rumus kerucut. Dalam rumus sendiri terdapat perhitungan volume yang memuat luas alas. Sedangkan dalam perhitungan luas terdapat penggunaan luas permukaan di dalamnya. Untuk itu luas permukaan dan volume kerucut dapat dicari menggunakan rumus lingkaran sebagai bentuk alasnya. Nah pada kesempatan kali ini saya akan menjelaskan tentang rumus luas permukaan kerucut, rumus volume kerucut dan contoh soal kerucut. Untuk lebih jelasnya dapat anda simak di bawah ini.
Contents
Rumus Kerucut (Luas Permukaan dan Volume) Beserta Contoh Soal
Seperti yang telah saya jelaskan di atas bahwa kerucut dapat disebut juga dengan limas. Namun bentuk alasnya saja yang berbeda karena alas kerucut berbentuk lingkaran. Karena bentuk alas kerucut ini berbentuk lingkaran, maka menggunakan phi (Π) dan jari jari dalam rumusnya.
Apa yang dimaksud kerucut itu? Pengertian kerucut ialah bangun tiga dimensi yang mempunyai dua sisi berupa sisi lengkung dan sisi lingkaran. Dalam kerucut tersebut terdapat garis pelukis (disimbolkan huruf s) yang bentuknya berupa sisi lengkung. Kemudian adapula lingkaran yang berperan serta dalam rumus di dalamnya.
Sebelum membagikan rumus kerucut, rumus luas permukaan kerucut, rumus volume kerucut dan contoh soal kerucut. Saya akan menjelaskan terlebih dahulu mengenai sifat sifat kerucut. Bangun ruang kerucut memiliki beberapa sifat di dalamnya seperti di bawah ini:
- Memiliki dua sisi yang berupa sisi lengkung dan lingkaran (sisi alasnya).
- Memiliki alas kerucut yang bentuknya lingkaran.
- Memiliki selimut kerucut yang bentuknya bidang lengkung.
- Bidang lengkungnya berupa sektor atau juring lingkaran.
- Memiliki satu rusuk.
- Memiliki satu titik puncak.
Rumus Luas Permukaan Kerucut
Kerucut memiliki luas permukaan dari alas kerucut yang digabungkan dengan selimut kerucut. Kerucut tersebut memiliki alas yang berupa bidang lingkaran dimana memiliki luas alas (πr²) dan jari jari (r). Luas permukaan ini dapat dirumuskan dalam bentuk seperti di bawah ini:
Luas permukaan kerucut = Luas alas + Luas selimut
Luas permukaan kerucut = πr² + πrs
Luas permukaan kerucut = πr (r + s)
Rumus Luas Selimut Kerucut
Selain rumus luas permukaan kerucut di atas. Adapula rumus kerucut yang berupa rumus luas selimut kerucut. Apabila terdapat bentangan selimut kerucut, maka selimut ini akan memiliki bentuk sektor atau juring lingkaran dimana keliling alas lingkarannya sama dengan busur. Untuk lebih jelasnya perhatikan gambar kerucut seperti di bawah ini:
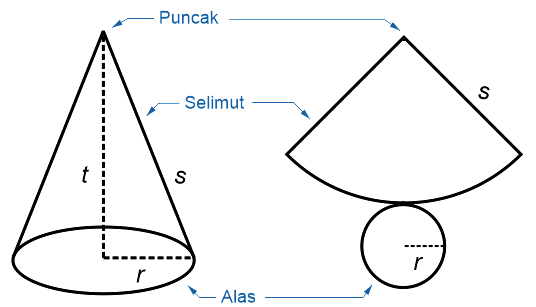
Berdasarkan gambar di atas dapat kita lihat adanya garis pelukis yang dilambangkan dengan huruf s. Pengertian garis pelukis ialah sisi tegak dari ujung atas yang panjangnya melengkung hingga ke bawah. Dari gambar tersebut terlihat pembentukan segitiga siku siku yang berasal dari tinggi, garis pelukis dan jari jari. Tinggi dan jari jari yang bertemu ini akan membentuk sudut siku siku. Maka dari itu luas selimut kerucutnya dapat dirumuskan menggunakan teorema pythagoras seperti di bawah ini:
s² = r² + t²
Rumus Volume Kerucut
Selain pengertian kerucut, sifat sifat kerucut, rumus luas permukaan kerucut dan rumus luas selimut kerucut di atas. Adapula rumus kerucut lainnya yang berupa rumus volume bangun kerucut. Kerucut memiliki volume yang dapat dirumuskan seperti di bawah ini:
Volume Kerucut = 1/3 x Luas Alas x Tinggi
Volume Kerucut = πr²t
Untuk menghitung luas alas kerucutnya dapat dilakukan dengan menggunakan rumus πr². Dimana π ialah phi dengan nilai pendekatan konstanta berupa 3,14 atau 22/7 dan r berupa jari jari lingkaran.
Contoh Soal Kerucut
Setelah menjelaskan tentang pengertian kerucut, sifat sifat kerucut, rumus luas permukaan kerucut, rumus luas selimut kerucut dan rumus volume kerucut di atas. Selanjutnya saya akan membagikan contoh soal terkait rumus kerucut tersebut. Berikut contoh soal dan pembahasannya yaitu:
1. Diketahui sebuah kerucut memiliki garis pelukis yang panjangnya 50 cm dan jari jari 28 cm. Tentukan luas selimut kerucutnya?
Pembahasan.
Luas selimut kerucut = πrs
= 22/7 x 28 x 50
= 4400 cm²
Jadi luas selimut kerucut tersebut ialah 4400 cm².
2. Diketahui diameter alas kerucut panjangnya 28 cm dengan garis pelukis 12 cm. Tentukan luas permukaan kerucut tersebut?
Pembahasan.
Contoh soal kerucut tersebut dapat diselesaikan dengan rumus seperti di bawah ini:
Luas permukaan kerucut = πr (r + s)
= 22/7 x 14 (14 + 12)
= 44(26)
= 1144 cm²
Jadi luas permukaan kerucut tersebut ialah 1144 cm².
Bagaimana contoh soal kerucut di atas, mudah bukan? Soal soal terkait bangun kerucut ini tentunya mudah untuk diselesaikan, karena kerucut memiliki rumus volume dan luas permukaannya sendiri. Maka dari itu penting sekali memahami bagaimana rumus kerucut tersebut, baik rumus volume maupun rumus luas permukaan.
Demikianlah penjelasan mengenai rumus luas permukaan kerucut, rumus volume kerucut dan contoh soal kerucut. Selain rumus kerucut tersebut, saya juga membahas tentang pengertian kerucut dan sifat sifat kerucut. Semoga artikel ini dapat bermanfaat dan terima kasih telah membaca materi kerucut di atas.


