Rumus Invers Matriks Beserta Contoh Soalnya – Pada umumnya SPLTV (Sistem Persamaan Linear Tiga Variabel) dalam Matematika dapat diselesaikan dengan menggunakan metode invers matriks dan determinan. Kita harus mencari determinan matriks terlebih dahulu sebelum menghitung invers matriks. Apa yang dimaksud determinan? Determinan merupakan perhitungan nilai yang berasal dari unsur matriks persegi.
Apakah anda tahu pengertian invers matriks itu? Invers dapat diartikan sebagai kebalikan atau lawan dari matriks. Matriks yang mempunyai invers dapat dinamakan dengan matriks nonsingular. Kemudian matriks yang tidak mempunyai invers dapat disebut dengan matriks singular. Bagaimana rumus invers matriks? Bagaimana cara menyelesaikan contoh soal invers matriks?
Invers matriks memang merupakan kebalikan dari dua matriks. Jika matriks tersebut dikalikan maka akan terbentuk matriks persegi (AB = BA = |). Invers matriks memiliki simbol berbentuk pangkat -1, dimana penulisannya diatas hurufnya. Misalnya matriks A merupakan invers matriks B, maka penulisannya dapat berbentu A = B¯¹. Matriks A dan matriks B tersebut saling berkebalikan (invers). Pada kesempatan kali ini saya akan menjelaskan tentang rumus invers matriks beserta contoh soal invers matriks. Untuk lebih jelasnya dapat anda simak di bawah ini.
Contents
Rumus Invers Matriks Beserta Contoh Soalnya
Secara umum invers matriks dapat dibedakan menjadi dua jenis yakni invers matriks berordo 2 x 2 (matriks persegi) dan matriks berordo 3 x 3. Kedua jenis matriks ini pada dasarnya memiliki rumus invers yang berbeda. Hal ini dikarenakan ordo yang dimiliki oleh kedua matriks ini juga tidak sama.
Seperti yang kita tahu bahwa tidak semua matriks mempunyai matriks. Matriks yang memiliki invers dapat dinamakan dengan matriks nonsingular, sedangkan matriks yang tidak memiliki invers dinamakan matriks singular. Invers matriks sendiri memiliki beberapa sifat seperti di bawah ini:
- Sebuah matriks A merupakan matriks bujur sangkar.
- Matriks A memiliki invers yakni A¯¹, apabila det(A) tidak sama dengan 0.
- Matriks A tidak mempunyai invers, apabila det(A) sama dengan 0.
Baca juga : Cara Menghitung Relasi dan Fungsi Beserta Contoh Soal Terlengkap
Invers Matriks Ordo 2 x 2
Saat mempelajari rumus matriks kalian harus menyesuaikan dengan ordonya. Ordo 2 x 2 menurut saya jadi jenis yang paling sederhana dan muda kita jumpai di buku. Berbagai contoh soal matriks invers ordo 2×2 pun tertulis rapi pada buku latihan siswa
Meski telah memperoleh porsi pembahasan dengan waktu yang cukup. Tapi tak semua mampu menghafal rumus matriks invers persegi tersebut. Maka dari itu, dalam sesi pertama akan saya jelaskan rumus invers matriks ordo 2 x 2 secara lengkap.

Apakah anda tahu cara menyelesaikan contoh soal invers matriks ordo 2 x 2 ini? Cara memperoleh invers matriks berordo 2 x 2 dapat dilakukan dengan langkah langkah seperti di bawah ini:
- Elemen yang terdapat dalam diagonal utama saling ditukarkan.
- Elemen elemen lainnya diberikan tanda negatif.
- Kemudian masing masing elemen dibagi dengan determinannya.
itulah rumus invers matriks 2×2 yang dapat saya sampaikan secara singkat. Materi tidak hanya berhenti di sini, karena masih ada matriks ordo 3×3 yang notabenya mempunyai rumus hitung lebih kompleks.
Invers Matriks Ordo 3 x 3
Cara mengerjakan soal invers matriks ordo 3×3 tidaklah semudah membalik telapat tangan. Sebab rumus matriks invers 3×3 cukup kompleks dan memiliki perbedaan signifikan dari apa yang saya ajarkan sebelumnya.
Selanjutnya saya akan menjelaskan tentang rumus invers matriks berordo 3 x 3. Matriks ordo 3 x 3 tersebut dapat dicari inversnya dengan menggunakan metode transformasi baris elementer dan metode adjoin.
Apa itu adjoin matriks? Pengertian adjoin matriks adalah transpose matriks yang elemen didalamnya termasuk dalam kofaktor elemen matriks itu sendiri. Matriks berordo 3 x 3 tersebut dapat dicari inversnya menggunakan rumus seperti di bawah ini:

Baca juga : Rumus Penjumlahan Matriks dan Pengurangan Matriks Beserta Contoh Soal
Matriks An dapat dicari inversnya menggunakan metode transformasi baris elementer dengan mengikuti beberapa langkah seperti di bawah ini:
- Matriks ini berbentuk (An|ln), dimana ln adalah matriks identitas dengan ordo n.
- Matriks (An|ln) ditransformasikan ke bentuk (ln|Bn) menggunakan transformasi elemen baris.
- Langkah kedua tersebut akan menghasilkan invers matriks An yakni Bn.
Selain rumus invers matriks di atas. Adapula beberapa notasi dalam transformasi baris elementer yang digunakan yaitu meliputi:
- Bi ↔ Bj merupakan penukaran elemen baris ke I menuju elemen baris ke j.
- Bi merupakan pengalihan masing masing elemen baris ke I bersamaan dengan skalar k.
- Bi + kBj merupakan penjumlahan k dengan elemen baris ke I serta dikalikan dengan elemen garis ke j.
Contoh Soal Invers Matriks
Ada banyak sekali model serta bentuk latihan soal invers matriks ordro 2×2 ataupun 3×3 yang dapat kita kerjakan. Selain dari buku pedoman matematika, siswa juga harus mencari tambahan referensi sendiri. Beruntungnya, internet menyediakan kebutuhan siswa untuk nelajar memperdalam ilmu serta pemahaman.
Setelah menjelaskan tentang rumus invers matriks di atas. Selanjutnya saya akan membagikan contoh soal matriks terkait rumus tersebut. Adapun contoh soal dan pembahasannya yaitu sebagai berikut:
Tentukan invers matriks di bawah ini!
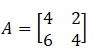
Pembahasan.
Contoh soal invers matriks tersebut dapat diselesaikan dengan cara seperti berikut:
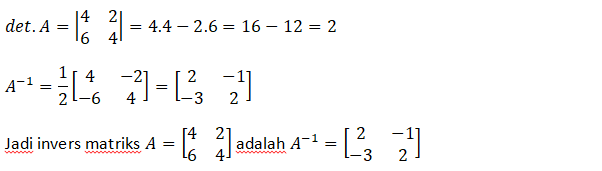
Sekian penjelasan mengenai rumus invers matriks beserta contoh soal invers matriks. Invers matriks merupakan kebalikan dari sebuah matriks. Semoga artikel ini dapat bermanfaat dan terima kasih telah membaca materi invers matriks di atas.


