Rumus Diskriminan Pada Persamaan Kuadrat Beserta Contoh Soalnya – Diskriminan dalam Matematika merupakan sebuah nilai yang dijadikan penentu sifat sifat dalam akar persamaan kuadrat. Kita dapat menentukan bentuk persamaan kuadrat dengan nilai ini, dimana penyelesaian yang dimilikinya berbentuk akar real atau tidak. Diskriminan juga termasuk dalam hubungan antar koefisien pada persamaan kuadrat untuk menentukan akar persamaan dan ciri ciri lainnya.
Materi diskriminan ini pada umumnya telah diajarkan ketika di bangku sekolah. Biasanya materi tersebut berkaitan dengan materi persaaan kuadrat. Meski sudah dijelaskan sedemikian rupa, namun masih ada siswa yang belum mengetahui bagaimana cara mencari nilai diskriminan tersebut. Apakah anda tahu pengertian diskriminan itu? Bagaimana rumus diskriminan pada persamaan kuadrat? Bagaimana cara menyelesaikan contoh soal diskriminan? Diskriminan secara umum adalah sebuah nilai pada persamaan kuadrat yang digunakan untuk membedakan jumlah akar dalam persamaan itu sendiri. Maka dari itu jenis jenis akar persamaan kuadrat dapat ditentukan dengan menggunakan diskriminan ini.
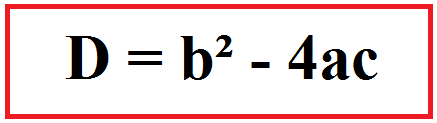
Apa itu persamaan kuadrat? Persamaan kuadrat adalah persamaan yang bentuknya ax² + bx + c = 0, dimana a, b, dan c merupakan konstanta yang berhubungan dengan persamaan kuadrat. Lantas bagaimana cara menghitung diskriminan pada persamaan kuadrat? Pada kesempatan kali ini saya akan menjelaskan tentang rumus diskriminan pada persamaan kuadrat dan contoh soal diskriminan. Untuk lebih jelasnya dapat anda simak di bawah ini.
Contents
Rumus Diskriminan Pada Persamaan Kuadrat Beserta Contoh Soalnya
Seperti yang kita tahu bahwa diskriminan secara umum merupakan sebuah nilai dalam persamaan kuadrat yang digunakan untuk membedakan jumlah akar pada persamaan tersebut. Maka dari itu nilai diskriminan dapat digunakan untuk menentukan jenis akar pada persamaan kuadrat.
Persamaan kuadrat tersebut merupakan persamaan Matematika yang mempunyai variabel dengan derajat paling tinggi dua. Kuadrat tersebut berfungsi untuk menyelesaikan masalah yang berhubungan dengan proyektil sehingga kurvanya seperti lintasan benda jatuh. Puncak paling tinggi sebuah benda yang dilempar atau kecepatan bola di lintasaan parabola dapat dihitung menggunakan fungsi kuadrat terebut.
Baca juga : Satu Tahun Berapa Minggu? Berikut Jawabannya
Persamaan kuadrat memiliki ciri ciri seperti pangkat tertinggi yang dimiiki variabel adalah 2, koefisien pada variabel berpangkat dua tidak sama dengan nol, sedangkan koefisien pada variabel berpangkat nol atau berpangkat 1 dapat bernilai 1. Di bawah ini terdapat rumus diskriminan pada persamaan kuadrat beserta contoh soal diskriminan. Berikut penjelasan selengkapnya:
Rumus Diskriminan
Nilai diskriminan dalam persamaan kuadrat ax² + bx + c = 0 dapat ditentukan dengan rumus seperti di bawah ini:
D = b² – 4ac
Keterangan:
D = Diskriminan
a = Koefisien variabel x²
b = Koefisien variabel x
c = Konstanta
Selain rumus di atas, adapula fungsi dan sifat sifat diskriminan pada persamaan kuadrat ax² + bx + c = 0 dimana a ≠ 0 yaitu sebagai berikut:
- Persamaan kuadrat memiliki dua akar nyata yang berlainan (x1 ≠ x2) apabila nilai D > 0.
- Persamaan kuadrat memiliki dua akar yang rasional, sama dan real (x1 = x2) apabila nilai D = 0.
- Persamaan kuadrat memiliki dua akar yang tidak real atau imajiner apabila nilai D < 0.
Baca juga : Jenis Jenis Prisma Lengkap Dengan Sifat Sifatnya
Contoh Soal Diskriminan
Setelah menjelaskan tentang pengertian diskriminan dan rumus diskriminan di atas. Selanjutnya saya akan membagikan contoh soal terkait rumus tersebut. Berikut contoh soal dan cara menghitung dikriminan yang benar yaitu:
1. Hitunglah nilai diskriminan dan jenis akar pada persamaan kuadrat x² – 12x + 18 = 0?
Jawab.
x² – 12x + 18 = 0, dimana a = 1, b = -12, dan c = 18
Maka,
D = b² – 4ac
D = (-12)² – 4(1)(9)
D = 144 – 72
D = 72
Jadi nilai diskriminannya adalah 72 dengan jenis akar rasional karena nilai D > 0 (72 > 0).
2. Tentukan jenis akar pada persamaan kuadrat x² + 8x +10?
Jawab.
x² + 8x + 10 = 0, dimana a = 1, b = 8, dan c = 10
Maka,
D = b² – 4ac
D = (8)² – 4(1)(10)
D = 64 – 40
D = 24
Jadi jenis akar pada persamaan kuadrat tersebut adalah rasional karena nilai D > 0 (24 > 0).
Demikianlah penjelasan mengenai rumus diskriminan pada persamaan kuadrat dan contoh soal diskriminan. Cara menghitung diskriminan tersebut sebenarnya mudah dilakukan karena hanya berpedoman pada rumus dan sifat sifat yang dimilikinya. Semoga artikel ini dapat bermanfaat dan terima kasih telah berkunjung di blog ini.