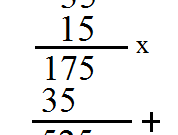Materi Perkalian Bentuk Akar Beserta Contoh Soal dan Pembahasan

Materi Perkalian Bentuk Akar Beserta Contoh Soal dan Pembahasan – Dalam Matematika terdapat pembelajaran mengenai akar. Akar dalam Matematika tersebut memiliki bentuknya sendiri. Bentuk akar Matematika ialah sebuah bilangan yang tidak tergolong dalam bilangan irasional dan bilangan rasional. Bilangan irasional ialah bilangan yang tidak pernah berhenti hasil baginya. Sedangkan bilangan rasional ialah bilangan yang mencakup bilangan prima, bilangan cacah dan bilangan lainnya. Akar dalam Matematika ini memiliki beberapa operasi hitung. Salah satunya ialah operasi hitung perkalian akar. Bagaimana bentuk contoh soal perkalian bentuk akar itu? Bagaimana cara menyelesaikan perkalian akar?

Bentuk akar dalam Matematika dapat diartikan sebagai sebuah bentuk yang menyatakan bilangan berpangkat. Bentuk akar ini dinyatakan dalam bentuk bilangan irasional yang tidak sama dengan b bilangan bulat a (b ≠ 0), bilangan a, dan bilangan pecahan a/b. Dalam bentuk akar ini terdapat sebuah bilangan yang disertai dengan tanda akar (√). Contohnya √3, √8, √12, dan sebagainya. Akan tetapi √16 tidak dapat dinyatakan sebagai bentuk akar. Hal ini dikarenakan √16 dapat dicari nilainya yaitu 4 dan 4 adalah bilangan rasional. Setelah mengenal bagaimana bentuk akar tersebut, selanjutnya kita akan membahas materi perkalian akar. Bagaimana materi perkalian bentuk akar itu?

Perkalian Bentuk Akar

Christoff Rudoff merupakan seorang Matematikawan dari Jerman yang pertama kali memperkenalkan simbol akar (√). Pemilihan simbol akar ini hampir sama dengan huruf “r” dari kata “radix” sesuai dengan penjelasan dalam bukunya berjudul Die Coss. Berdasarkan bahasa latin, kata radix memiliki makna berarti akar pangkat dua. Pada kesempatan kali ini saya akan menjelaskan tentang materi perkalian bentuk akar beserta contoh soal perkalian bentuk akar dan pembahasan. Untuk lebih jelasnya dapat anda simak di bawah ini.

Materi Perkalian Bentuk Akar Beserta Contoh Soal dan Pembahasan

Sifat Sifat Bentuk Akar

Bagaimana cara menyederhanakan bentuk akar itu? Bentuk akar dapat disederhanakan dengan sifat, dimana a dan b ialah bilangan positif rasional. Kemudian untuk materi perkalian bentuk akar tersebut memiliki ketentuan sifat yang berkebalikan dengan penyederhanan bentuk akar. Adapun sifat perkalian bentuk akar yaitu. Agar anda lebih memahami bagaimana cara menyelesaikan perkalian akar tersebut, maka dapat anda simak contoh soal yang akan saya bagikan ini. Berikut contoh soal perkalian bentuk akar yaitu sebagai berikut:

Contoh Soal

Sederhanakan bentuk akar di bawah ini:
1. √3 x √5
2. √2 x √11
3. √5 x √13
4. √3 x √11

Jawab.
1. √3 x √5 = √(3 x 5) = √15
2. √2 x √11 = √(2 x 11) = √22
3. √5 x √13 = √(5 x 13) = √65
4. √3 x √11 = √(3 x 11) = √33

Contoh soal perkalian bentuk akar di atas merupakan perkalian akar yang sederhana. Akan tetapi bagaimana jika bentuk akar yang dikalikan berupa a√b × c√d? Untuk materi perkalian bentuk akar a√b × c√d memiliki sifat tertentu yaitu. Agar anda lebih memahami perkalian pada bentuk akar tersebut, maka perhatikan contoh soal berikut ini:

Contoh Soal

Sederhanakan bentuk akar di bawah ini:
1. 3√3 x 2√5
2. 4√2 x 3√11
3. 2√5 x 5√13
4. 3√3 x 2√11

Jawab.
1. 3√3 x 2√5 = (3 x 2)√(3 x 5) = 6√15
2. 4√2 x 3√11 = (4 x 3)√(2 x 11) = 12√22
3. 2√5 x 5√133 = (2 x 5)√(5 x 13) = 10√65
4. 3√3 x 2√11 = (3 x 2)√(3 x 11) = 6√33