Contoh Soal Kesebangunan Segitiga dan Jawabannya – Materi kesebangunan dan kekongruenan memang sudah tidak asing lagi dalam ilmu Matematika. Materi ini memiliki pengertian dan cara pengerjaan yang berbeda. Bahkan sifat sifat kesebangunan dan sifat sifat kekongruenan tersebut juga berbeda. Apa yang dimaksud kesebangunan itu? Apakah anda tahu sifat sifat kesebangunan tersebut? Kesebangunan atau lebih sering disebut sebangun ialah sudut sudut yang sesuai sehingga besarnya sama. Dalam kesebangunan tersebut terdapat ukuran antara satu bangun dengan bangun lainnya memiliki besar sudut yang sama sehingga perbandingan sisi sisi yang bersesuaian tersebut sama.
Bagaimana cara menyelesaikan contoh soal kesebangunan segitiga itu? Materi kesebangunan tersebut sering muncul dalam soal soal ujian Matematika, baik ujian Nasional maupun ujian sekolah. Materi kesebangunan tersebut sebenarnya termasuk dalam ilmu geometri. Dalam materi tersebut seringkali digabungkan dengan jenis bangun bangun datar seperti segitiga, trapesium maupun persegi panjang. Cara menyelesaikan kesebangunan bangun datar tersebut pada umumnya hampir sama. Untuk itu meskipun bentuknya tidak sama, namun cara mengerjakannya menggunakan konsep yang sama.
Apa yang dimaksud kesebangunan itu? Pengertian kesebangunan ialah kesesuaian sudut sudut pada bangun datar yang besarnya sama. Kemudian panjang sisi sisi pada sudutnya juga memiliki perbandingan yang sama. Maka dari itu bangun datar dinyatakan sebangun apabila sudut dan panjang sisi bersesuaiannya memiliki perbandingan sama. Pada kesempatan kali ini saya akan membagikan contoh soal kesebangunan segitiga dan jawabannya. Untuk lebih jelasnya dapat anda simak di bawah ini.
Contoh Soal Kesebangunan Segitiga dan Jawabannya
Seperti yang kita tahu bahwa kesebangunan sendiri berbeda dengan kekongruenan. Kesebangunan lebih mengarah pada kesesuaikan ukuran dan sudut pada dua bangun atau lebih. Sedangkan kekongruenan lebih mengarah pada persamaan sudut dan ukuran beberapa bangun.
Kesebangunan bangun datar dapat dilambangkan dengan notasi yang berbentuk ≈. Kesebangunan sendiri dapat didefinisikan sebagai kesesuaian sudut dalam bangun datar yang memiliki besar sama. Seperti yang sudah saya katakan di atas bahwa kesebangunan memiliki sifat sifat di dalamnya. Adapun sifat sifat kesebangunan bangun datar yang terbentuk yaitu:
- Sepasang sisi yang bersesuaian memiliki perbandingan yang sama.
- Sudut sudut yang bersesuaian memiliki persamaan yang sama besar.
Baca juga : Contoh Soal Domain Fungsi, Rumus, dan Cara Menentukannya
Dua bangun datar dapat dinyatakan sebagun apabila perbandingan panjang sudut dan sisi yang bersesuaian tersebut besarnya sama. Bentuk bangun datar yang dapat memanfaatkan konsep kesebangunan tersebut dapat berupa segitiga dan trapesium. Di bawah ini terdapat contoh soal kesebangunan segitiga beserta jawabannya yaitu meliputi:
1. Perhatikan gambar berikut!
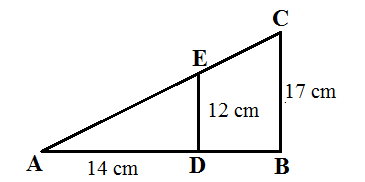
Tentukan panjang DB?
Jawaban.
Dalam gambar di atas terdapat dua segitiga yang sebangun yaitu segitiga ADE dan ABC. Segitiga ABC memiliki ukuran yang lebih besar daripada segitiga ADE. Untuk menentukan panjang DB dapat dilakukan dengan menggunakan sisi sisi bersesuaian. Namun kita harus menentukan terlebih dahulu mengenai panjang AB seperti di bawah ini:
AB / BC = AD / DE
AB / 17 = 14 / 12
AB = (14 x 17) / 12
AB = 19,83 cm
Maka,
Panjang DB = AB – AD = 19,83 – 14 = 5,83 cm
Jadi panjang DB ialah 5,83 cm.
2. Perhatikan gambar berikut!
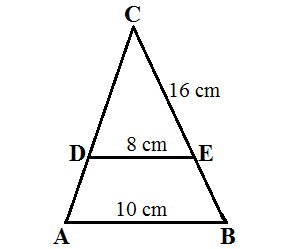
Hitunglah panjang BE dan BC?
Jawaban.
Contoh soal kesebangunan segitiga di atas dapat diselesaikan dengan cara seperti berikut:
BC / AB = EC / DE
BC / 10 = 16 / 8
BC = (16 x 10) / 8
BC = 20 cm
Maka,
Panjang BE = BC – EC = 20 – 16 cm = 4 cm
Jadi panjang BE = 4 cm dan panjang BC = 20 cm.
Baca juga : Rumus Penjumlahan Pecahan Biasa dan Campuran Beserta Contohnya
3. Perhatikan gambar berikut!
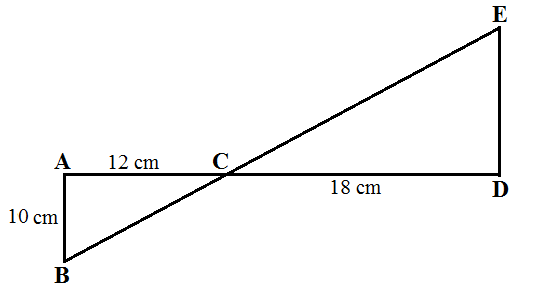
Tentukan panjang DE?
Jawaban.
DE / DC = AB / AC
DE / 18 = 10 / 12
DE = (10 x 18) / 12
DE = 15 cm
Jadi panjang DE ialah 15 cm.
4. Perhatikan gambar berikut!
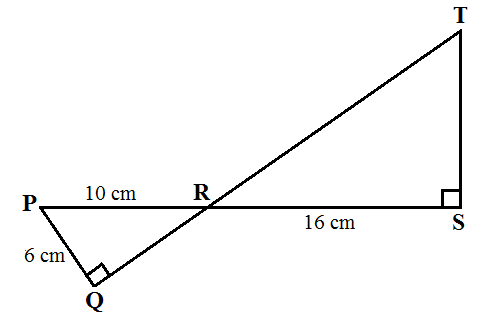
Hitunglah panjang ST?
Jawaban.
Contoh soal kesebangunan segitiga di atas dapat diselesaikan dengan mencari panjang QR terlebih dahulu. Panjang QR tersebut dapat ditentukan menggunakan konsep teorema phytagoras seperti di bawah ini:
QR² = PR² – PQ²
QR² = 10² – 6²
QR² = 100 – 36
QR² = 64
QR = √64
QR = 8 cm
Setelah itu menentukan panjang ST dengan metode berikut:
ST / SR = PQ / QR
ST / 16 = 6 / 8
ST = (6 x 16) / 8
ST = 12 cm
Jadi panjang ST ialah 12 cm.
Ada banyak sekali variasi latihan soal kesebangunan segitiga kelas 9, 7 atau bahkan untuk mereka di jenjang SMA. Masing-masing tentu memiliki tingkat kesulitan berbeda sesuai level para siswa. Selama dapat menghafal rumus hitung yang tepat saya yakin kalian tak akan menjumpai kesulitan pada saat mengerjakan.
Sekian contoh soal kesebangunan segitiga dan jawabannya yang dapat saya bagikan. Segitiga merupakan salah satu bangun datar yang sering digunakan dalam konsep kesebangunan. Apabila kamu memperoleh kesulitan pada saat mengerjakan jangan sungkan untuk meninggalkan pertanyaan di kolom komentar. Semoga artikel ini dapat bermanfaat dan terima kasih telah berkunjung di blog ini.


