Pengertian Bilangan Bulat, Operasi Hitung dan Contoh – Apa yang dimaksud bilangan bulat itu? Apa saja operasi hitung bilangan bulat itu? Bagaimana contoh bilangan bulat? Dalam ilmu Matematika tentunya terdapat pembahasan mengenai materi bilangan. Apa pengertian bilangan itu? Bilangan secara umum dapat diartikan sebagai konsep Matematika yang digunakan dalam proses pencacahan dan pengukuran.
Bilangan tersebut secara umum memang dilambangkan dalam bentuk angka sebagai wakilnya. Bilangan Matematika memang selama bertahun tahun memiliki konsep yang luas, maka bilangan ini terbagi menjadi beberapa jenis seperti bilangan nol, bilangan rasional, bilangan negatif, bilangan irasional dan bilangan kompleks. Selain itu adapula jenis bilangan lainnya yaitu bilangan bulat.
Ketika masuk materi bilangan bulat kita akan berjumpa dengan beberapa pembahasan yang menurut saya lumayan kompleks. Siswa harus bisa menghafal pengertian bilangan bulat, menghafal rumus operasi hitung bilangan bulat, serta mengerjakan contoh soal secara benar. Uniknya, bilangan bulat sebenarnya termasuk dalam jenis bilangan rasional selain bilangan pecahan.
Bilangan bulat merupakan himpunan bilangan yang mengandung bilangan satu, bilangan komposit, bilangan genap, bilangan prima, bilangan nol, bilangan ganjil, bilangan asli, bilangan negatif dan bilangan cacah. Bilangan bulat pada umumnya berasal dari bilangan negatif yang digabungkan dengan bilangan cacah. Bilangan bulat ini memiliki simbol berupa huruf Z dari Bahasa Jerman yaitu Zahlen yang maknanya bilangan.
Contents
Pengertian Bilangan Bulat, Operasi Hitung dan Contoh
Istilah mengenai bilangan tentunya sudah tidak asing lagi di dunia Matematika. Terlebih lagi materi bilangan ini telah diajarkan ketika memasuki jenjang pendidikan sekolah dasar. Materi dasar Matematika yang perlu dipahami ialah materi bilangan ini. Hal ini dikarenakan konsep bilangan Matematika memang digunakan dalam melakukan pencacahan dan pengukuran.
Sederhananya, bilangan dapat digunakan untuk memaparkan banyaknya atau jumlah objek tertentu. Lalu apa yang dimaksud bilangan bulat itu? Pada kesempatan kali ini saya akan menjelaskan tentang pengertian bilangan bulat, operasi hitung bilangan bulat dan contoh bilangan bulat. Untuk lebih jelasnya dapat anda simak di bawah ini.
Pengertian Bilangan Bulat
Apakah anda tahu apa pengertian bilangan itu? Bilangan memang merupakan sebuah konsep untuk melakukan suatu pengukuran dan pencacahan. Bilangan ini secara sederhana berguna untuk menjelaskan suatu jumlah atau banyak objek. Salah satu jenis bilangan tersebut ialah bilangan bulat. Bilangan bulat memang dapat diartikan sebagai bilangan satu (1), bilangan komposit, bilangan genap (2, 4, 6, 8, …), bilangan prima (2, 3, 5,7, …), bilangan nol (0), bilangan ganjil (1, 3, 5, 7, 9, …), bilangan asli (1, 2, 3, 4, 5, …), bilangan negatif (-1,-2, -3, -4, …) dan bilangan cacah (0, 1, 2, 3, 4, …).
Dari pengertian bilangan bulat di atas kita tahu gambaran mengenai materi bilangan bulat tersebut. Kita dapat menulis himpunan bilangan bulat dalam bentuk seperti berikut { . . ., -4, -3, -2, -1, 0, 1, 2, 3, 4, …}. Lambang bilangan bulat memang berasal dari Bahasa Jerman yaitu “Zahlen” yang maknanya bilangan sehingga simbolnya dapat berupa huruf Z. Pengurutan dan penulisan bilangan bulat pada dasarnya menggunakan garis bilangan. Garis bilangan tersebut berguna untuk melakukan operasi hitung bilangan bulat.
Bilangan bulat pada dasarnya memiliki ciri khas tersendiri untuk membedakannya denga jenis bilangan Matematika lainnya. Dalam bilangan bulat tersebut memuat bilangan negatif, bilangan nol dan bilangan positif di dalamnya. Agar anda lebih paham mengenai materi bilangan bulat ini, maka saya akan membagikan beberapa contoh dan operasi hitung bilangannya. Di bawah ini terapat penjelasan mengenai operasi hitung dan contoh bilangan bulat yaitu:
Contoh Pada Bilangan Bulat
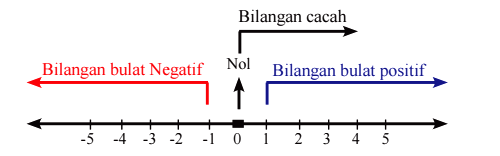
Bilangan bulat dapat kita amati dalam bentuk { . . ., -4, -3, -2, -1, 0, 1, 2, 3, 4, …}. Contoh dari bilangan bulat ini dapat dinyatakan dalam bentuk garis bilangan seperti berikut:
![]()
Berdasarkan garis bilangan di atas, kita dapat membagi bilangan bulat menjadi beberapa jenis. Adapun jenis jenis bilangan bulat yaitu:
- Bilangan bulat positif yaitu himpunan bilangan yang berupa 1, 2, 3, 4, 5, …. Bilangan ini juga dapat dinamakan dengan bilangan asli.
- Bilangan bulat negatif yaitu himpunan bilangan yang berupa -1, -2, -3, -4, …. Letak bilangan bulat negatif pada garis bilangan biasanya ada di sebelah kiri angka nolnya.
- Bilangan nol ialah bilangan yang memuat angka nol (0).
Operasi Hitung Bilangan Bulat
Setelah menjelaskan tentang pengertian bilangan bulat dan contoh bilangan bulat di atas. Selanjutnya saya akan membahas tentang operasi hitung pada materi bilangan bulat. Bilangan bulat memuat beberapa operasi hitung di dalamnya seperti pengurangan, pembagian, penjumlahan dan perkalian. Berikut penjelasan selengkapnya:
Operasi Penjumlahan
Operasi hitung bilangan bulat yang pertama ialah operasi penjumlahan. Operasi hitung ini menggunakan tanda “+” di dalamnya. Penjumlahan sebuah bilangan pada garis bilangan dengan bilangan positif lainnya akan menghasilkan gerakan ke arah kanan sehingga nilainya semakin besar. Adapun beberapa sifat operasi penjumlahan bilangan bulat yaitu:
- Sifat komutatif atau pertukaran yang bentuknya a + b = b + a.
- Sifat asosiatif atau pengelompokan yang bentuknya (a + b) + c = a + (b + c).
- Unsur identitas yang berupa bilangan nol sehingga bentuknya dapat berupa 0 + a = a + 0.
- Unsur invers yang berupa invers a = -a, invers -a = a sehingga penulisannya dapat berupa a + (-a) = 0.
- Sifat tertutup yaitu sifat penjumlahan yang menghasilkan bilangan bulat pula sehingga bentuknya berupa a + b = c, dimana a, b dan c ialah bilangan bulat.
Operasi Pengurangan
Selain pengertian bilangan bulat dan contoh bilangan bulat di atas. Adapula operasi hitung bilangan bulat berupa pengurangan. Operasi ini biasanya menggunakan tanda “-” di dalamnya. Pengurangan bilangan pada garis bilangan dengan bilangan positif lainnya akan menghasilkan gerakan ke arah kiri sehingga nilainya semakin kecil. Adapun beberapa sifat operasi pengurangan yaitu:
- a – b = a + (-b)
- a – (-b) = a + b
- Tidak memberlakukan sifat asosiatif ((a – b) – c ≠ a – (b – c)) dan sifat komutatif (a – b ≠ b – a).
- Berhubungan dengan bilangan nol sehingga bentuknya berupa a – 0 = a atau 0 – a = -a.
- Sifat tertutup yaitu sifat pengurangan yang menghasilkan bilangan bulat pula sehingga bentuknya berupa a – b = c, dimana a, b dan c ialah bilangan bulat.
Operasi Perkalian
Operasi perkalian bilangan bulat pada umumnya menggunakan tanda “×” di dalamnya. Perkalian tersebut dapat dinamakan dengan penjumlahan berulang. Di bawah ini terdapat sifat sifat perkalian bilangan bulat yaitu:
- a x b = ab
- a x (-b) = -ab
- (-a) x (-b)= ab
- a x b = b x a (sifat komutatif)
- (a x b) x c = a x (b x c) (sifat asosiatif)
- a x (b + c) = ab + ac (sifat distributif)
- a x 1 = a (unsur identitas)
- Sifat tertutup yaitu sifat perkalian yang menghasilkan bilangan bulat pula sehingga bentuknya berupa a x b = c, dimana a, b dan c ialah bilangan bulat.
Operasi Pembagian
Selain pengertian bilangan bulat dan contoh bilangan bulat di atas. Adapula operasi hitung bilangan bulat berupa pembagian. Bilangan bulat ini memiliki beberapa sifat di dalamnya seperti:
- (+) : (+) = (+)
- (+) : (-) = (-)
- (-) : (-) = (+)
- Pembagian dengan bilangan nol yang menghasilkan nilai tidak terdefinisi (a : 0 = tidak terdefinisi).
- Tidak memberlakukan sifat asosiatif ((a : b) : c ≠ a : (b : c)) dan sifat komutatif (a : b ≠ b : a).
Sekian penjelasan mengenai pengertian bilangan bulat, operasi hitung bilangan bulat dan contoh bilangan bulat. Bilangan bulat memiliki operasi hitung di dalamnya seperti operasi pengurangan, pembagian, penjumlahan dan perkalian. Semoga artikel ini dapat bermanfaat dan terima kasih telah membaca materi bilangan bulat di atas.


